動的ドレープ理論
複合積層材構造は、一般的に、型の表面に対して必要な方向に補強プライを配置することによって形成されます。
平坦なサーフェスおよび一方向に湾曲したサーフェスの場合は、実質的にプライの方向が適用領域全体で変化しません。二方向に湾曲したサーフェスになると、プライは変形することによってのみサーフェスに沿うことができます。特に、予め含漬させた乾燥した織物は、過剰な力を加えなくても二方向に湾曲したサーフェスの形状にフィットすることができます。変形は面内せん断で発生し、特定の変形レベルまで、繊維のせん断剛性はごくわずかです。[1]
プライがせん断によってサーフェスに沿って変形すると、繊維方向が変化します。いわゆるドレーププロセスのシミュレーション用に、さまざまなアプローチが開発されました。[2] ドレープシミュレーションには2つのニーズがあります。第一に、複合材製品の製造可能性を評価できます。補強ではサーフェスに沿うことができない領域が指摘されるため、設計時点で対策を講じてこれを回避することができます。第二に、ドレープシミュレーションは、モデル内の任意の場所における実際の繊維方向を示すことができます。この情報は、構造の正確な有限要素解析に不可欠です。
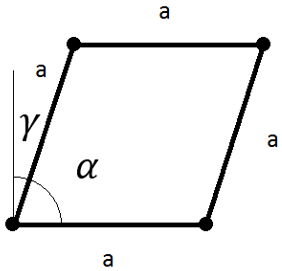
図 1.
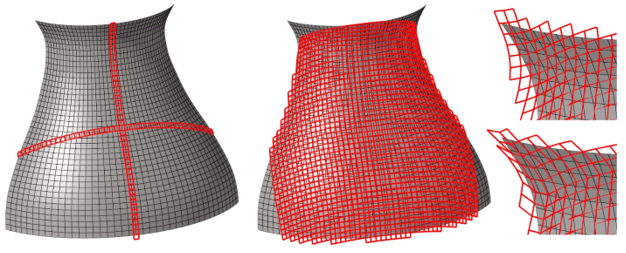
図 2.
既知の節点が2つの要素のドレープ(左)。ドレープ伝播は、最初の直交方向に行われます。既知の節点が3つの要素のドレープ(中央)。適用範囲は、主なドレープパスに基づきます。ドレープの再開(右)と完全な適用。再開時は、デフォルトの緩和角度が最初に使用されます。次に、最大緩和角度が使用されます。関連モデルRevolution.hmがインストールのtutorials\hmフォルダーにあります。
ここから、2つの節点の位置は、反復最小化アルゴリズムを使用して決定できます。
ドレープシミュレーションは、指定されたシードポイントから開始され、指定されたドレープ方向に進行します。このフェーズで、各ドレープ要素には最初に既知の節点が2つずつあります。ドレープ要素は、モデルエッジに到達するまで並べられます。この手順は、最初は直交している4つすべての主方向(デフォルトでオンに設定される)で同時に進行します。主方向のドレープと並行して、既知の節点が3つのドレープ要素が入力されます。アルゴリズムにより、モデル全体がドレープされるかどうか、または、ドレープシミュレーションを再開する必要がある領域が存在するかどうかが決定されます。
再開は、ドレープパッチエッジの中央から開始されます。再開の位置では、2つの節点が既知で、2つの未知の節点をエネルギー最小化を使用して決定する必要があります。通常、この解析では、制限されることなく、非常に緩やかなドレープメッシュが生成されます。ユーザーは、緩和角度パラメータ(デフォルトは3度)を使用してドレープメッシュのリカバリを制御できます。このパラメータは、その親ドレープ要素に基づいて緩和のレベルを制限します。その後、アルゴリズムにより問題のエッジでドレープ要素の列がスイープされ、他のドレープされていないエッジなどに進みます。
このシミュレーションによって、繊維の主方向1(縦糸)と主方向2(横糸)が決定されます。ドレープされた繊維方向1は、適宜材料方向を修正するための有限要素モデルにマップされます。織りプライは、それぞれの方向が0度と90度の2つの一方向プライに分割され、別々にドレープすることができます。
これは、理想的な非せん断ケースからの逸脱を表しています。モデルサーフェス上のβ値を可視化すると、問題領域を描く際に役立ちます。せん断値は、有限要素メッシュにマップされ、絶対値として使用できます。ほとんどの繊維補強で、最大変形角αは30~40度です。[6] 繊維が特定の変形レベルにせん断されている場合は、せん断力が急激に増加し始め、せん断変形ではほとんど増加しません。この制限はロッキング角度と呼ばれます。この制限を超えると、座屈が確認される可能性があります。Kinematic Drapingダイアログでは、βのデフォルト値が55度に設定されます。補強のロッキング角度は実験的に決定することができます。[7]
ピンジョイントネットモデルは、特に、織物用に開発されたものですが、変形が穏やかな場合のクロスプライプリプレグスタックや単一の一方向プライに対しても機能することが実証されています。[8]

図 3.
参考資料
- Deep drawing of fabric reinforced thermoplastics, Bergsma OK, Huisman J., In: Brebbia CA, de Wilde WP, Blain WR, editors.Computer aided design in composite material technology, New York: Springer, 1988. p. 323-334.
- Algorithms for draping fabrics on doubly-curved surfaces, Van der Ween F., Int J Numer Meth Eng 1991;31:1415-1426.
- The influence of accurate stretch data for reinforcements on the production of complex structural moldings.Part 1.Deformation of aligned sheets and fabrics, Potter KD., Composites 1979;10: 161-167.
- The draping of woven fabric preforms and prepregs for production of polymer composite components, Wang J et al.Composites: Part A 30 (1999) 757-765.
- Fabric draping simulation in composites manufacturing Part II.Analytical methods, Van West BP, Luby SC., J Adv Mater 1997;28(3):36-41.
- Experimental studies and analysis of the draping of woven fabrics, Mohammed U et al.Composites: Part A 31 (2000) 1409-1420.
- On the relationship between shear angle and wrinkling of textile composite preforms, Prodromou AG, Chen J. Composites: Part A 28A (1997) 491-503.
- Bias extension measurements on cross-plied unidirectional prepreg, Potter K. Composites: Part A 33 (2002) 63-73.
- Fitting a woven-cloth model to a curved surface: mapping algorithms, Aono M., Breen D.E. and Wozny M.J., Computer-Aided Design, Volume 26, Issue 4, April 1994, 278-292.
- A Geometry Information Based Fishnet Algorithm for Woven Fabric Draping in Liquid Composite Molding, Yang B, Jin T., Bi F. and Li J., ISSN 1392–1320 Materials Science (MEDŽIAGOTYRA).Vol. 20, No. 4.2014.