acker
Ackermann's formula (pole placement gain selection for single-input systems).
Syntax
K = acker(A, B, P)
Inputs
- A
- The state matrix (n x n), where n is the number of states.
- B
- The input matrix (n x 1).
- P
- The desired closed-loop pole location vector.
Outputs
- K
- Feedback gain matrix K.
Example
A=[0 1;20.6 0];
B=[0;1];
C=[1 0];
D=[0];
t = 0:0.01:2; %Time Vector
u = zeros(size(t)); %Input vector
x0 = [0.01 0]; %Initial Condition
%-----Closed loop Poles location
p1 = -1.80000 + 2.40000i;
p2 = -1.80000 - 2.40000i;
K = acker(A,B,[p1 p2])
sys_cl = ss(A-B*K,B,C,0);
lsim(sys_cl,u,t,x0); %Simulate time response of dynamic system to arbitrary inputs
xlabel('Time (sec)');
ylabel('Ball Position (m)');
grid;K = [Matrix] 1 x 2
29.60000 3.60000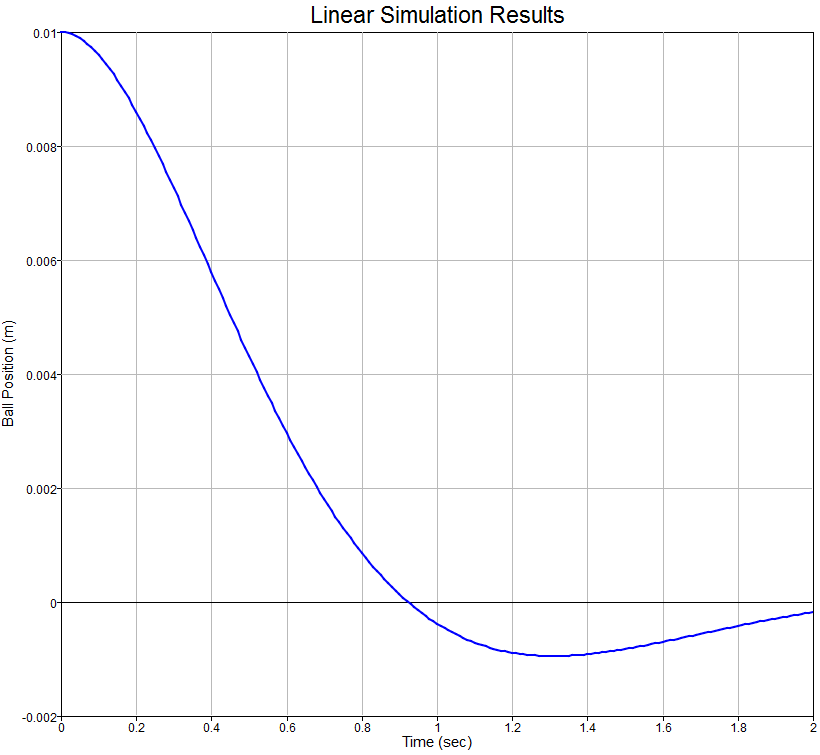
Comments
K = acker(A, B, P) computes the feedback gain matrix K such that the single input systemx = Ax + Bu with a feedback law of u = -K * x has the closed loop poles specified in vector P, with P = eig(A - B * K).