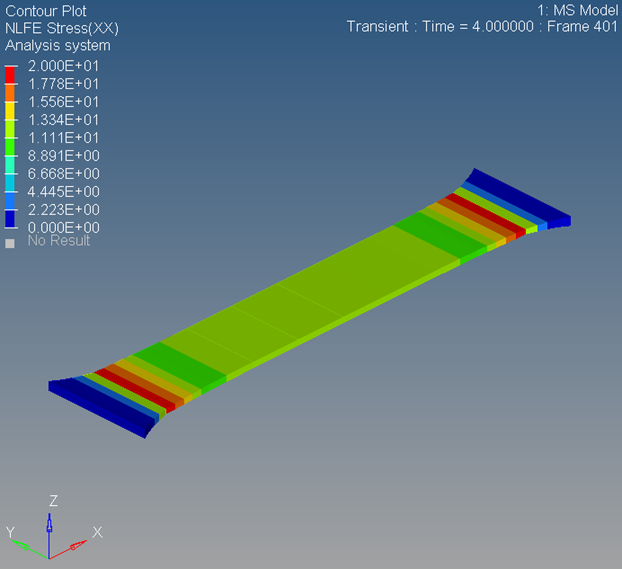
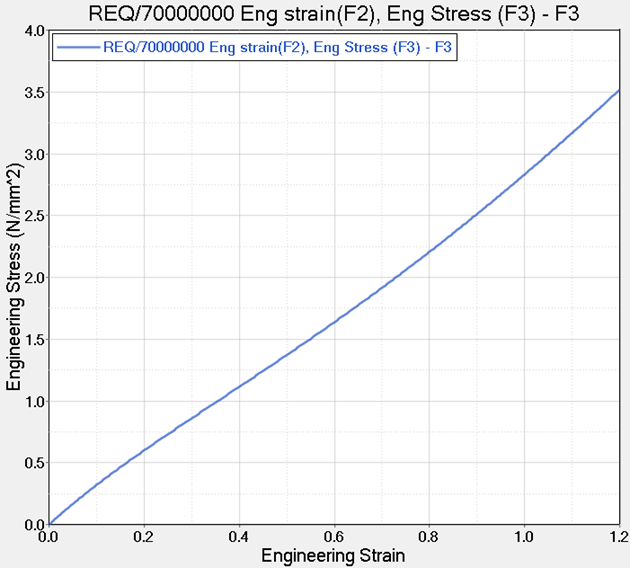
Exercise 2: Tensile Test of Elastomer
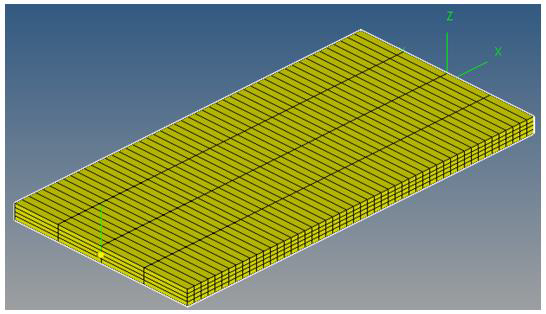
In this exercise, you will perform a uni-axial tensile test on a rubber strip (2mmx5mmx50mm).
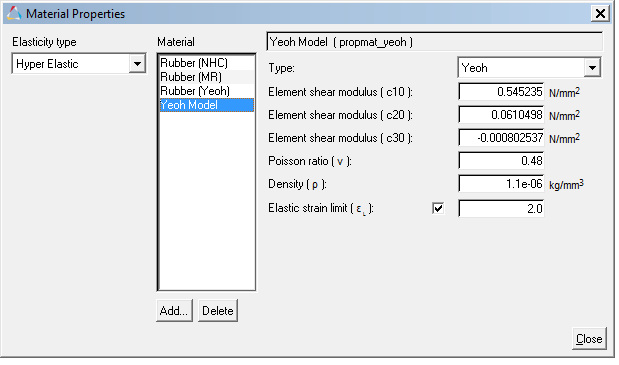
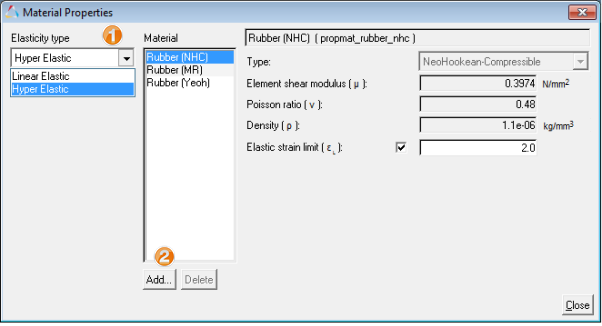
Hyper-elastic material constants have been sourced from reference[3].
Hyper-elastic materials are large strain materials when compared to metals. In case of hyper-elastic materials the non-linear relation between stress and strain is derived from a strain energy density function. Currently MotionSolve supports three hyper-elastic material models: Neo-Hookean, Mooney–Rivlin, and Yeoh.
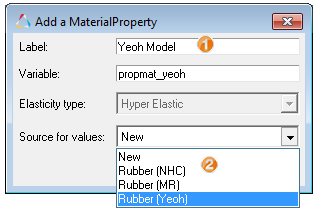
Add a New Material Property
In this step, you will add a new material property.
Model the Rubber Strip
In this step, you will model the rubber strip for the tensile test.
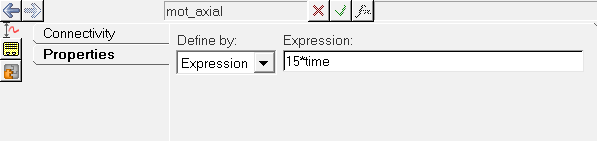
Add Constraints
In this step, you will create constraints for the rubber strip model.
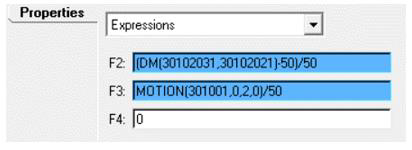
Add Outputs
Now you will create outputs to measure engineering strain and engineering stress values.
Engineering Strain = 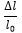
Engineering Stress = 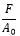
Solve and Post-Process the Model
References
JUSSI T, SOPANEN and AKI M. MIKKOLA:
Description of Elastic Forces in Absolute Nodal Coordinate Formulation. Journal of Nonlinear Dynamics 34: 53– 74, 2003.
Oleg Dmitrochenko:
Finite elements using absolute nodal coordinates for large deformation flexible multibody dynamics. Proceedings of the Third International Conference on Advanced Computational Methods in Engineering (ACOMEN 2005).
Sung Pil Jung, TaeWon Park, Won Sun Chung:
Dynamic analysis of rubber like material using absolute nodal coordinate formulation based on the non-linear constitutive law. Journal of Nonlinear Dyn (2011) 63: 149–157.
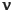 ):
): 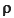 ):
):