Generic Heat Exchanger Component

Generic Heat Exchanger Description and Quick Guide

The Generic Heat Exchanger requires that the heat exchanger performance is known. There are several options to specify the performance such as: temperature change, thermal duty, NTU, effectiveness, and the Hs parameter.

Generic Heat Exchanger can be used in Compressible and Incompressible (hydraulic and non-hydraulic) simulations. Currently no phase change is available. The component has four fluid connections, and it models heat exchange between two streams in a network. Heat Exchangers in Flow Simulator come with 4 hidden chambers representing the 4 sides of a heat exchanger. The Generic Heat Exchanger uses Orifice or Effective Area elements (Compressible or Incompressible) in the backend to model restrictions losses (pressure loss) of both flow paths based on user defined loss parameters and characteristic flow area. The Heat addition/removal is calculated based on user inputs for Heat Exchanger Performance curves in Generic Hx module and Q (Heat Addition/Removal) is supplied to Orifice or Effective Area Elements to predict temperatures of the exiting fluids.

Some of the important modeling aspects to be taken care while using heat exchanger components are:

The Hot Side circuit must get connected to Line 1 (Indicated by Red Color part of Component Image) & Cold Side circuit get connected to Line 2 (Indicated with Blue Color part of Component Image) as shown in the image below.
You can choose to model additional inlet and outlet losses using the separate Discrete Loss/Tube Element upstream and downstream of heat exchanger respectively.
The Hot/Cold Side circuit line must be connected with either compressible or Incompressible set of elements. Mixing of elements sets for a Hot/Cold side circuit line is not allowed. Below Table represents some modelling/Allowable scenarios.

Modeling/Allowable Scenarios	Flow Simulator Network
Hot Side: Compressible Gases Cold Side: Compressible Gases Example: Air to Air Heat Exchanger
Hot Side : Incompressible Liquids Cold Side : Incompressible Liquids Example: Fuel Cooled Oil Cooler (FCOC)
Hot Side: Incompressible Liquids Cold Side: Compressible Gases Example: Air Cooled Oil Cooler (ACOC)
Hot Side: Compressible Gases Cold Side: Incompressible Liquids Example: Air to Liquid Heat Exchanger

Flow Simulator can also be used for Heat Exchanger design. For heat exchanger design a detailed representation of the heat exchanger is required. The example below shows flow elements representing the cold and hot side with thermal network resistors connecting the sides. Heat exchanger performance can be predicted from such a model.

Generic Heat Exchanger Element Inputs

Table of the inputs for the Generic Heat Exchanger Component.

Element Specific Generic Heat Exchanger Component Input Variables
Index	UI Name (.flo label)	Description
3,11	Cross Sectional Area (AREA_COLD, AREA_HOT)	Flow area for hot & cold side fluids
4,12	Hydraulic Diameter (HYD_DIA_COLD, HYD_DIA_HOT)	Hydraulic Diameter for hot & cold side fluids
5,13	Pressure Loss Options (PLOSS_COLD, PLOSS_HOT)	Options to specify type of pressure loss modelling Fixed Loss Coefficient Fixed Total Pressure Drop Flow vs Delta.P (PTIN – PSEX) Velocity vs Delta.P (PTIN – PSEX) Loss Coefficient vs Reynolds Number
6,14	Loss Coefficient (KLOSS_COLD, KLOSS_HOT)	Incompressible Loss Coefficient
7,15	Delta Total Pressure (DELTA_PT_COLD, DELTA_PT_HOT)	Total pressure drop across a flow path
T1, T2, T3, T4	Flow vs Delta P (COLD_DELTA-P, COLD_FLOW, HOT_DELTA-P, HOT_FLOW)	User Specified Curve for Flow vs Delta.P. Delta-P table is the DIFFERENCE between the upstream driving total pressure and downstream sink static pressure
T1, T2, T3, T4	Fluid Velocity vs Delta P (COLD_DELTA-P, COLD_VEL, HOT_DELTA-P, HOT_VEL)	User Specified Curve for Fluid Velocity vs Delta.P. Delta-P table is the DIFFERENCE between the upstream driving total pressure and downstream sink static pressure
T1, T2, T3, T4	Loss Coefficient vs Reynolds Number (COLD_KLOSS, COLD_REYN, HOT_ KLOSS, HOT_REYN)	User Specified Curve for Loss Coefficient vs Reynolds Number. $R e y n o l d s N u m b e r = (4.0 * W / (P E R I M * μ))$ Where: $μ = D y n a m i c V i s c o s i t y$ $W = M a s s F l o w R a t e$ $P E R I M = P e r i m e t e r = U s e r I n p u t$ If Hydraulic Diameter is provided, then: $P e r i m e t e r = 4.0 * A / H Y D D I A M$ If Hydraulic Diameter or Perimeter is not Provided, Reynolds number is calculated based on Orifice Area: $P e r i m e t e r = \sqrt{(4.0 * D P I * A)}$
25	Heat Transfer Options (HOPT)	Options for Modelling Heat Transfer between Hot & Cold side Fluids Thermal Duty: Heat Input Hot Fluid Delta.T Cold Fluid Delta.T Effectiveness Effectiveness vs Flow_Rate_Cold vs Flow_Rate_Hot Effectiveness vs NTU vs Heat Capacity Ratio Nusselt Number vs RE_Cold vs RE_Hot Constant hA coefficient value 14) Hs Constant 15) Hs vs Flow_Rate_Cold vs Flow_Rate_Hot
26	Heat Input (QIN)	Heat Addition
27	Fluid Delta.T (DELT_T)	Delta Total Temperature for Hot (or Cold) Side fluid
28	Effectiveness (EFFECTIVENESS)	Effectiveness of Heat Exchanger
T4, T5, T6	Effectiveness vs Flow_Rate_Cold vs Flow_Rate_Hot (FLOWRATE_COLD, FLOW_HOT.., EFFECTIVENESS)	3d Table for Effectiveness vs Flow_Rate_Cold vs Flow_Rate_Hot
T4, T5, T6	Effectiveness vs NTU vs Heat Capacity Ratio (NTU, ..HEAT_RATIO, EFFECTIVENESS)	3d Table for Effectiveness vs NTU vs Heat Capacity Ratio
T7, T8, T9	Nusselt Number vs RE_Cold vs RE_Hot (NusseltNumber, ReynoldsCold, ReynoldsHot)	3d Nusselt Number vs RE_Cold vs RE_Hot
37	Overall Heat Transfer Coefficient (OVERALL_HTC)	Overall Heat Transfer Coefficient Input
29	Type of Configurations (CONFIG_TYPE)	Heat Exchangers Flow Configurations Parallel Flow Counter Flow Shell & Tube Cross flow both flows unmixed Cross flow One fluid mixed
31	Primary hA coefficient (PRI_HA)	Htc*Area Coefficient of Primary side fluid
32	Secondary hA coefficient (SEC_HA)	Htc*Area Coefficient of Secondary side fluid
30	Number of Shell Passes (NUM_SHELL_PASS)	No of Shell Passes for Shell & Tube Hx Configurations
40	Select Mixed Flow (MIXED_FLOW)	Mixed Flow side of HX for Cross flow one side mixed option. 1=Primary, 2=Secondary
41	HX Area (HX_AREA)	The total heat exchanger area to be used with the Hs performance parameter
42	Hs Parameter (HS_PARAMETER)	A Heat Exchanger Performance Parameter

Generic Heat Exchanger Theory Manual

Nomenclature:
$W$ : Mass flow rate	C: Heat Capacity
$ρ$ : Density	Q: Heat Addition/Rejection
$C p$ : Specific Heat	Tt: Total Temperature
NTU: Number of Transfer Units
Subscripts:
in, up, 1: Upstream station	C: Cold
ex, dn, 2: Downstream station	H: Hot

Pressure Loss Calculations

There are five different options through which pressure loss across hot or Cold stream can be modelled. They are:

Fixed Loss Coefficient
Fixed Total Pressure Drop
Flow vs Delta.P (PTIN – PSEX)
Velocity vs Delta.P (PTIN – PSEX)
Loss Coefficient vs Reynolds Number

As discussed above, Generic Heat Exchanger uses Orifice or Effective Area elements (Compressible or Incompressible) in the backend to model restrictions losses (pressure loss).

To get more details on pressure drop calculation for:

Fixed Loss Coefficient and Fixed Pressure Drop input refer to the Orifice Documentation.
Curve based inputs (3,4,5) mentioned above refer to the Effective-Area Orifice Documentation

Heat Transfer Calculations

Heat Input (Qin)
$T_{t, e x, C o l d} = T_{t, i n, C o l d} + \frac{Q i n}{W_{C o l d} * C p_{a v g, C o l d}}$

$T_{t, e x, H o t} = T_{t, i n, H o t} - \frac{Q i n}{W_{H o t} * C p_{a v g, H o t}}$
Hot Fluid Delta.T
$Q = W_{H o t} * C p_{a v g, H o t} (T_{t, i n, H o t} - T_{t, e x, H o t})$

$T_{t, e x, C o l d} = T_{t, i n, C o l d} + \frac{Q}{W_{C o l d} * C p_{a v g, C o l d}}$
Cold Fluid Delta.T
$Q = W_{C o l d} * C p_{a v g, C o l d t} (T_{t, e x, C o l d} - T_{t, i n, C o l d})$

$T_{t, e x, H o t} = T_{t, i n, H o t} - \frac{Q}{W_{H o t} * C p_{a v g, H o t}}$
Effectiveness
$C_{H o t} = A B S (W_{H o t}) * C p_{a v g, H o t}$

$C_{C o l d} = A B S (W_{C o l d}) * C p_{a v g, C o l d}$

$C_{m i n} = m i n (C_{H o t}, C_{C o l d})$

$Q_{M a x} = C_{m i n} * (T_{h, i n} - T_{c, i n})$

$Q = Q_{M a x} * E f f e c t i v e n e s s$

$T_{t, e x, C o l d} = T_{t, i n, C o l d} + \frac{Q}{W_{C o l d} * C p_{a v g, C o l d}}$

$T_{t, e x, H o t} = T_{t, i n, H o t} - \frac{Q}{W_{H o t} * C p_{a v g, H o t}}$
Effectiveness vs Flow_Rate_Cold vs Flow_Rate_Hot
Effectiveness is obtained from User Defined Input for Effectiveness as function Flow_Rate_Cold and Flow_Rate_Hot.

$C_{H o t} = A B S (W_{H o t}) * C p_{a v g, H o t}$

$C_{C o l d} = A B S (W_{C o l d}) * C p_{a v g, C o l d}$

$C_{m i n} = m i n (C_{H o t}, C_{C o l d})$

$Q_{M a x} = C_{m i n} * (T_{h, i n} - T_{c, i n})$

$Q = Q_{M a x} * E f f e c t i v e n e s s$

$T_{t, e x, C o l d} = T_{t, i n, C o l d} + \frac{Q}{W_{C o l d} * C p_{a v g, C o l d}}$

$T_{t, e x, H o t} = T_{t, i n, H o t} - \frac{Q}{W_{H o t} * C p_{a v g, H o t}}$
Effectiveness vs NTU vs Heat Capacity Ratio
Effectiveness is obtained from User Defined Input for Effectiveness as function NTU and Heat Capacity Ratio.

$N T U = \frac{U A}{C_{m i n}}$

$C_{R a t i o} = \frac{C_{m i n}}{C_{m a x}}$

UA is calculated from Constant user input or from curve specified for Nusselt Number as function of Reynolds Number Cold and Reynolds Number Hot

$U A = \frac{N u s s e l t_N u m b e r * K}{D h}$

$E f f e c t i v e n e s s = 1 - e^{((\frac{1}{C_{R a t i o}}) N T U^{0.22} e^{(- C_{R a t i o} N T U^{0.78} - 1)})}$

$C_{H o t} = A B S (W_{H o t}) * C p_{a v g, H o t}$

$C_{C o l d} = A B S (W_{C o l d}) * C p_{a v g, C o l d}$

$C_{m i n} = m i n (C_{H o t}, C_{C o l d})$

$Q_{M a x} = C_{m i n} * (T_{h, i n} - T_{c, i n})$

$Q = Q_{M a x} * E f f e c t i v e n e s s$

$T_{t, e x, C o l d} = T_{t, i n, C o l d} + \frac{Q}{W_{C o l d} * C p_{a v g, C o l d}}$

$T_{t, e x, H o t} = T_{t, i n, H o t} - \frac{Q}{W_{H o t} * C p_{a v g, H o t}}$
Nusselt Number vs RE_Cold vs RE_Hot
Nusselt Number is obtained from User Defined Input for Nusselt Number as function of Reynolds Number Cold and Reynolds Number Hot

$U A = \frac{N u s s e l t_N u m b e r * K}{D h}$

$N T U = \frac{U A}{C_{m i n}}$

$E f f e c t i v e n e s s = 1 - e^{((\frac{1}{C_{R a t i o}}) N T U^{0.22} e^{(- C_{R a t i o} N T U^{0.78} - 1)})}$

$C_{H o t} = A B S (W_{H o t}) * C p_{a v g, H o t}$

$C_{C o l d} = A B S (W_{C o l d}) * C p_{a v g, C o l d}$

$C_{m i n} = m i n (C_{H o t}, C_{C o l d})$

$Q_{M a x} = C_{m i n} * (T_{h, i n} - T_{c, i n})$

$Q = Q_{M a x} * E f f e c t i v e n e s s$

$T_{t, e x, C o l d} = T_{t, i n, C o l d} + \frac{Q}{W_{C o l d} * C p_{a v g, C o l d}}$

$T_{t, e x, H o t} = T_{t, i n, H o t} - \frac{Q}{W_{H o t} * C p_{a v g, H o t}}$
Constant hA Coefficient value
$C_{H o t} = A B S (W_{H o t}) * C p_{a v g, H o t}$

$C_{C o l d} = A B S (W_{C o l d}) * C p_{a v g, C o l d}$

$C_{m i n} = m i n (C_{H o t}, C_{C o l d})$

$\frac{1}{U A} = {(\frac{1}{h * A})}_{C o l d} + {(\frac{1}{h * A})}_{H o t}$
NTU Effectiveness Methods:
1. Cross Flow Unmixed
  $E f f e c t i v e n e s s = 1 - e^{((\frac{1}{C_{R a t i o}}) N T U^{0.22} e^{(- C_{R a t i o} N T U^{0.78} - 1)})}$
2. Counter Flow
  $E f f e c t i v e n e s s = \frac{1 - e^{- N T U (1 - C_{R a t i o})}}{1 - C_{R a t i o} e^{- N T U (1 - C_{R a t i o})}}$
3. Parallel Flow
  $E f f e c t i v e n e s s = \frac{1 - e^{- N T U (1 + C_{R a t i o})}}{1 + C_{R a t i o}}$
4. Cross Flow Both Side Mixed
  $E f f e c t i v e n e s s = \frac{1}{\frac{1}{(1 - e^{_N T U})} + \frac{C_{R a t i o}}{1 - e^{- C_{R a t i o} N T U}} - \frac{1}{N T U}}$
5. Cross Flow One Side Mixed
  Cmin is mixed: $E f f e c t i v e n e s s = 1 - e^{- (\frac{1}{C_{R a t i o}}) (1 - e^{- C_{R a t i o} N T U})}$
  
  Cmax is mixed: $E f f e c t i v e n e s s = (\frac{1}{C_{R a t i o}}) (1 - e^{- (C_{R a t i o} (1 - e^{_N T U}))})$
  
  $Q_{M a x} = C_{m i n} * (T_{h, i n} - T_{c, i n})$
  
  $Q = Q_{M a x} * E f f e c t i v e n e s s$
  
  $T_{t, e x, C o l d} = T_{t, i n, C o l d} + \frac{Q}{W_{C o l d} * C p_{a v g, C o l d}}$
  
  $T_{t, e x, H o t} = T_{t, i n, H o t} - \frac{Q}{W_{H o t} * C p_{a v g, H o t}}$
Hs Parameter Methods (Constant and vs Hot and Cold Flowrates)
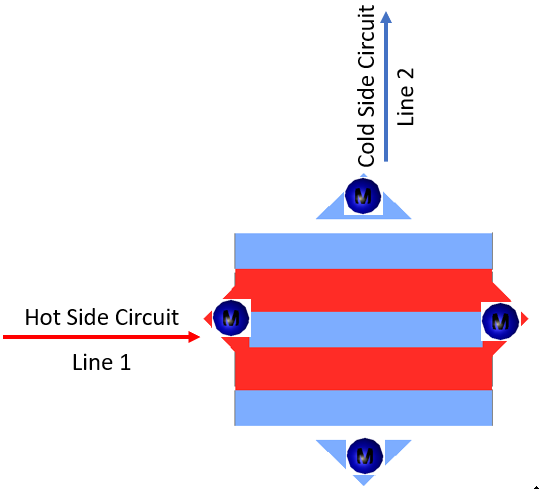
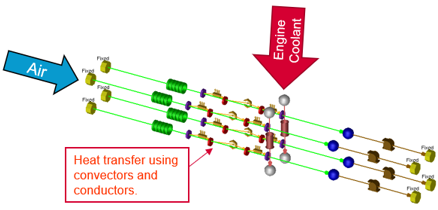
The Hs parameter is typically used to describe radiators where the hot side is a liquid coolant, and the cold side is air.

$H_{s} = \frac{A B S (W_{H o t}) * C p_{a v g, H o t} * (T_{h, i n} - T_{h, e x})}{H X_{A r e a} * (T_{h, i n} - T_{c, i n})}$

$H_{s} * H X_{A r e a} * (T_{h, i n} - T_{c, i n}) = A B S (W_{H o t}) * C p_{a v g, H o t} * (T_{h, i n} - T_{h, e x}) = Q$

A heat exchanger effectiveness can be calculated using the Hs parameter.

$E f f e c t i v e n e s s = Q / Q_{M a x}$

$Q_{M a x} = C_{m i n} * (T_{h, i n} - T_{c, i n})$

$E f f e c t i v e n e s s = \frac{H_{s} * H X_{A r e a} * (T_{h, i n} - T_{c, i n})}{C_{m i n} * (T_{h, i n} - T_{c, i n})} = \frac{H_{s} * H X_{A r e a}}{C_{m i n}}$

Q is found using the effectiveness Qmax. The Q is applied to the fluid streams to get the exit temperatures.

$T_{t, e x, C o l d} = T_{t, i n, C o l d} + \frac{Q}{W_{C o l d} * C p_{a v g, C o l d}}$

$T_{t, e x, H o t} = T_{t, i n, H o t} - \frac{Q}{W_{H o t} * C p_{a v g, H o t}}$

Note: Bi-Linear interpolation is employed between the values in the table to determine Y Values. If X-Value is less than its first value entry in the table, the first Y-Value entry is used. If X-Value is greater than its last value entry in the table, the last Y-Value entry is used. Flow Simulator doesn’t do any extrapolation if the values are outside the prescribed input limits.

Generic Heat Exchanger Outputs

The following listing provides details about Generic Heat Exchanger Component output variables.

Name	Description	Units
PS	Static pressure	psia, MPa
PT	Total pressure	psia, MPa
TT	Total temperature of fluid	deg F, deg K
RE	Reynold Number	(None)
Rho	Density	lbm/ft^3, Kg/m^3
CP	Specific Heat	Btu/(Lbm R), kJ/Kg.K
K	Thermal Conductivity	Btu/(hr ft R), W/m.K
DVISC	Dynamic Viscosity	Lbm/(hr ft), N s/m^2
Area	Flow Area	In2, m2
Heat Mode	Heat Mode Options (An echo of the user input) Heat Input Hot Fluid Delta.T Cold Fluid Delta.T Effectiveness Effectiveness vs Flow_Rate_Cold vs Flow_Rate_Hot Effectiveness vs NTU vs Heat Capacity Ratio Nusselt Number vs RE_Cold vs RE_Hot Constant hA coefficient value	(None)
Pri/cold_side_ploss_opt	Options specified for Pressure Loss Modelling for Pri/Cold side Fixed Loss Coefficient Fixed Total Pressure Drop Flow vs Delta.P (PTIN – PSEX) Velocity vs Delta.P (PTIN – PSEX) Loss Coefficient vs Reynolds Number (An echo of the user input)	(None)
Sec/hot_side_ploss_opt	Options specified for Pressure Loss Modelling for Sec/Hot side Fixed Loss Coefficient Fixed Total Pressure Drop Flow vs Delta.P (PTIN – PSEX) Velocity vs Delta.P (PTIN – PSEX) Loss Coefficient vs Reynolds Number (An echo of the user input)	(None)
Q	Heat Transferred between Heat Exchanger fluids.	BTU/sec, W
Effectiveness	Effectiveness of Heat Exchanger	(None)
Pri/cold_side_delta.p	Delta.PT on Pri/Cold side flow	psia, MPa
Sec/hot_side_delta.p	Delta.PT on Sec/Hot side flow	psia, MPa
Mdot	Mass Flow Rate	Lbm/s, kg/s
Flow configuration	Heat Exchangers Flow Configurations Parallel Flow Counter Flow Shell & Tube Cross flow both flows unmixed Cross flow One fluid mixed (An echo of the user input)	(None)
Overall conductance(UA)	Overall Thermal Resistance	BTU/hr.F, W/K
NTU	No of Transfer Units	(None)
Pri_hA_out	Pri/Cold side flow hA Coefficient value	BTU/hr.F, W/K
Sec_hA_out	Sec/Hot side flow hA Coefficient value	BTU/hr.F, W/K