RD-E: 1803 Square Membrane Elasto-Plastic

This example concerns the torsion problem of an embedded plate subjected to two concentrated loads. This example illustrates the role of different shell element formulations with regard to the mesh.

Options and Keywords Used

  • Q4 shells
  • T3 shells
  • Hourglass and mesh
  • Boundary conditions (/BCS)

    The boundary conditions are such that the three nodes of a single side and the two middle ones are blocked, while the others are free with respect to the Y axis.

  • Concentrated loads (/CLOAD)
    Two concentrated loads are applied on the corner points of the opposite side. They increase over time, as defined by the following function:
    F(t) 0 10 10
    t 0 200 400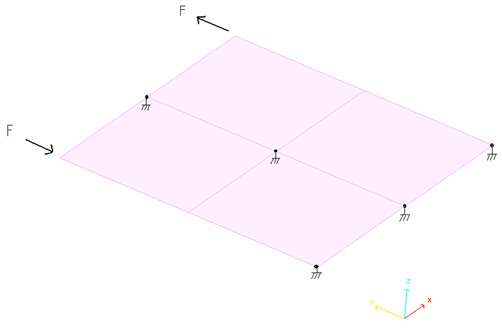

    rad_ex_fig_18-19
    Figure 1. Boundary Conditions and Loads

Input Files

The input files used in this example include:
4Q4
<install_directory>/hwsolvers/demos/radioss/example/18_Square_plate/Membrane_elasto-plastic/4Q4/.../TRACTION*
8T3
<install_directory>/hwsolvers/demos/radioss/example/18_Square_plate/Membrane_elasto-plastic/8T3/.../TRACTION*
8T3 inv
<install_directory>/hwsolvers/demos/radioss/example/18_Square_plate/Membrane_elasto-plastic/8T3_inv/.../TRACTION*
2Q4-4T3
<install_directory>/hwsolvers/demos/radioss/example/18_Square_plate/Membrane_elasto-plastic/2Q4-4T3/.../TRACTION*

Model Description

Units: mm, ms, g, N, MPa

The material used follows an isotropic elasto-plastic behavior with the Johnson-Cook plasticity model (/MAT/LAW2), with the following characteristics:
Material Properties
Initial density
7.8x10-3 [ g m m 3 ] MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaamWaaeaada WcaaqaaiaadEgaaeaacaWGTbGaamyBamaaCaaaleqabaGaaG4maaaa aaaakiaawUfacaGLDbaaaaa@3BBC@
Young's modulus
210000 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
Poisson ratio
0.3
Yield stress
206 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
Hardening parameter
450 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
Hardening exponent
0.5
Maximum stress
340 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@

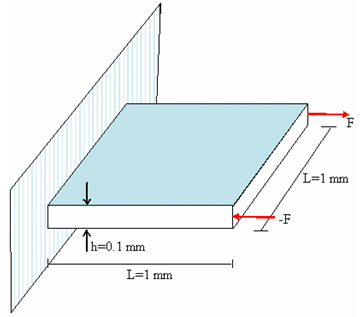
rad_ex_fig_18-17
Figure 2. Geometry of the Problem

Model Method

Four shells are modeled with different types of mesh:
Mesh 1
Two quadrilateral shells and four triangular shells (2Q4-4T3)
Mesh 2
Four quadrilateral shells (4Q4)
Mesh 3
Eight triangular shells (8T3)
Mesh 4
Eight triangular shells (8T3 inverse)
For each model, the following element formulation is tested:
  • QBAT formulation (Ishell =12)
  • QEPH formulation (Ishell =24)
  • Belytshcko & Tsay formulation (Ishell =1 or 3, hourglass control TYPE1, TYPE3)
  • C0 and DKT18 formulations

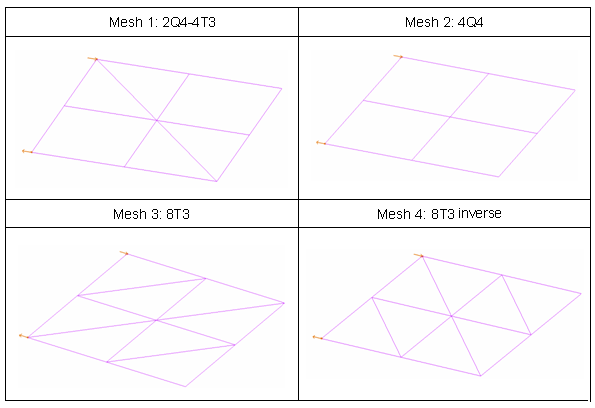
rad_ex_fig_18-18
Figure 3. Square Plate Meshes

Results

Curves and Animations

This example compares several models concerning:
  • the use of different element formulations for each mesh
  • the different types of mesh for a given element formulation
To compare the results, two criteria are used:
  • absorbed energy (internal and hourglass)
  • vertical displacement of the node under the loading point

The following diagrams summarize the results obtained.

Energy Curves / Comparison for Element Formulations

Mesh 1: 2Q4-4T3

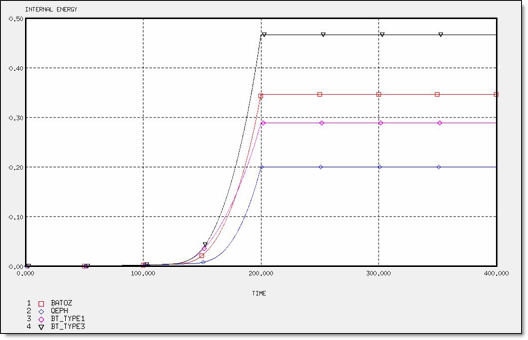
rad_ex_fig_18-20
Figure 4. Internal Energy for 2 x Q4 and 4 x T3 Elements

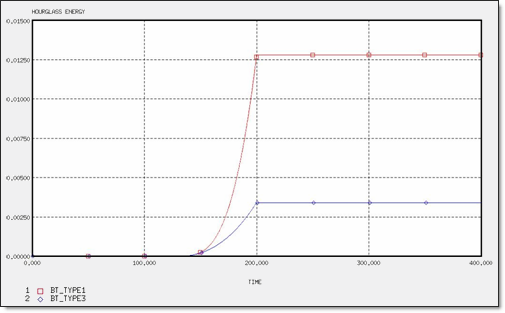
rad_ex_fig_18-21
Figure 5. Hourglass Energy for 2 x Q4 and 4 x T3 Elements

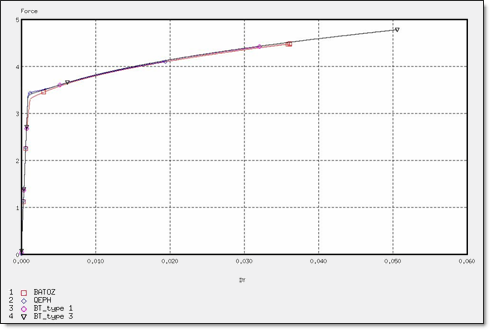
rad_ex_fig_18-22
Figure 6. Force for 4 x Q4 Elements
Mesh 2: 4Q4

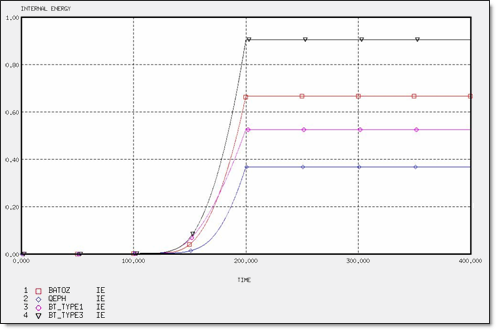
rad_ex_fig_18-23
Figure 7. Internal Energy for 4 x Q4 Elements

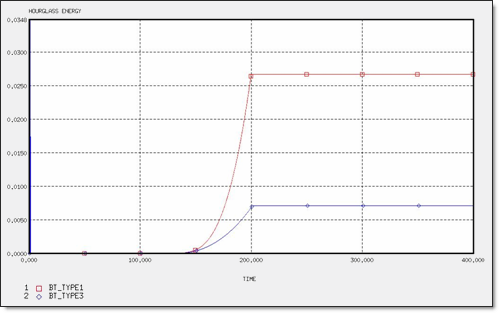
rad_ex_fig_18-24
Figure 8. Hourglass Energy for 4 x Q4 Elements

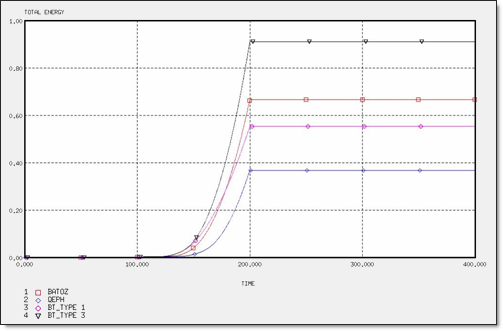
rad_ex_fig_18-25
Figure 9. Total Energy for 4 x Q4 Elements

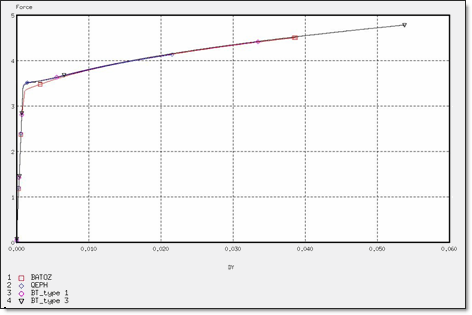
rad_ex_fig_18-26
Figure 10. Force for 4 x Q4 Elements

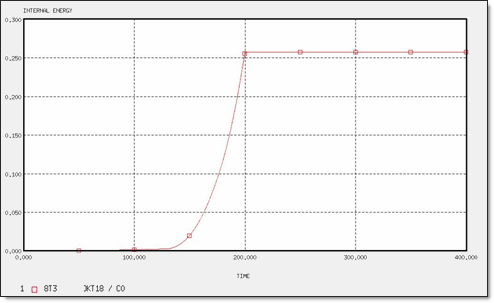
rad_ex_fig_18-27
Figure 11. Internal Energy for 8 x T3 Elements

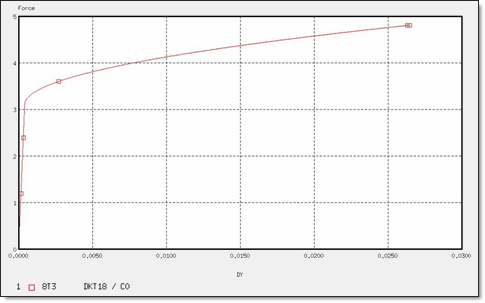
rad_ex_fig_18-28
Figure 12. Force for 8 x T3 Elements
Mesh 4: 8T3_INV

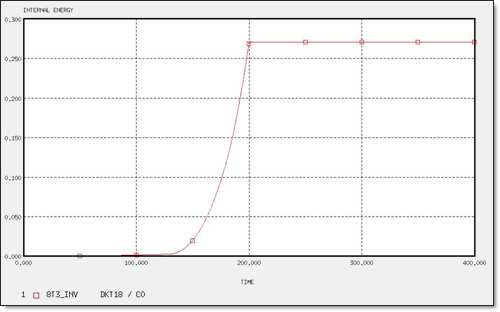
rad_ex_fig_18-29
Figure 13. Internal Energy for 8 x T3 Elements (inversed mesh)

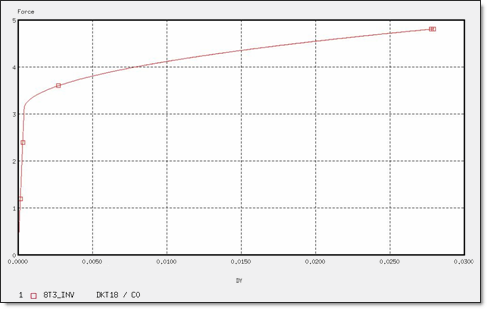
rad_ex_fig_18-30
Figure 14. Force for 8 x T3 Elements (inversed mesh)

Comparison for Different Meshes


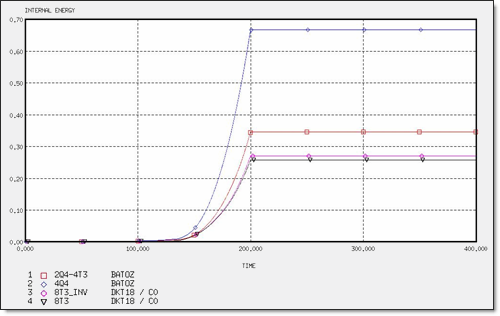
rad_ex_fig_18-31
Figure 15. Internal Energy for Different Meshes

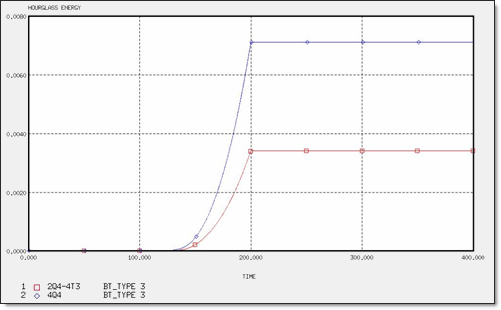
rad_ex_fig_18-32
Figure 16. Hourglass Energy for Different Meshes

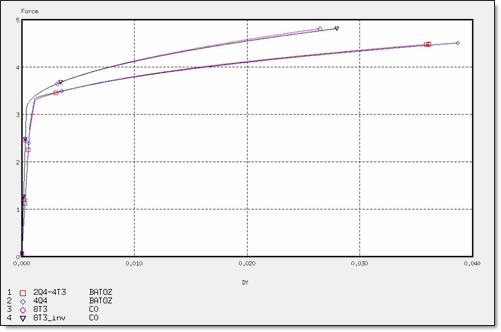
rad_ex_fig_18-33
Figure 17. Force for Different Meshes
Table 1. Displacement and Maximum Energy Comparison
Plastic 2Q4-4T3 4Q4 8T3 8T3_INV
QEPH BT_TYPE 1 BT_TYPE 3 BATOZ QEPH BT_TYPE 1 BT_TYPE 3 BATOZ DKT CO DKT CO
IEmax 2.37 x 10-1 2.89 x 10-1 3.03 x 10-1 3.46 x 10-1 2.69 x 10-1 5.27 x 10-1 5.67 x 10-1 6.67 x 10-1 2.57 x 10-1 2.57 x 10-1 2.70 x 10-1 2.70 x 10-1
HEmax -- 1.26 x 10-2 2.13 x 10-2 -- -- 2.66 x 10-2 4.41 x 10-2 -- -- -- -- --
Total Energy 2.37 x 10-1 3.02 x 10-1 3.24 x 10-1 3.46 x 10-1 2.96 x 10-1 5.54 x 10-1 6.11 x 10-1 6.67 x 10-1 2.57 x 10-1 2.57 x 10-1 2.70 x 10-1 2.70 x 10-1
Dymax 2.36 x 10-2 3.20 x 10-2 3.35 x 10-2 3.61 x 10-2 1.72 x 10-2 3.34 x 10-2 3.56 x 10-2 3.87 x 10-2 2.64 x 10-2 2.64 x 10-2 2.79 x 10-2 2.79 x 10-2
ε p max 2.76 x 10-2 3.78 x 10-2 3.97 x 10-2 4.43 x 10-2 1.87 x 10-2 3.72 x 10-2 3.97 x 10-2 4.50 x 10-2 6.28 x 10-2 6.28 x 10-2 6.28 x 10-2 6.28 x 10-2

Conclusion

The purpose of this example was to highlight the role of the elasto-plastic treatment when formulating Radioss shells. The in-plane plasticity was considered here. Regarding the applied boundary conditions and the Poisson effect on the plate, the test may be very severe with respect to the behavior of plastic in under-integrated elements.

In the case of a mesh with four quadrilaterals, the QBAT element always provides the best results as it allows four integration points to be put over the element. The plasticity computation over the integration points is thus more accurate. The under-integrated elements, having just one integration point at the center, allows only two integration points to be put through the width of the mesh. Another point concerns the role of Poisson's ratio in the plasticity computation. In fact, the QEPH element uses an analytical expression of the hourglass energy which takes into account the accurate expression in terms of the Poisson ratio (refer to the Radioss Theory Manual for further information). However, some approximations are induced in its elasto-plastic formulation, possibly influencing the results, especially for low levels of work-hardening. In the BT element formulation with a TYPE3 hourglass control, the Poisson ratio effect on the plastic part of the hourglass deformation is computed by a simplified expression which minimizes its role. In fact, the results obtained using BT_TYPE3 are slightly affected by the change in υ (use υ =0 for the example studied and compare the results obtained). The BT elements are generally more flexible and provide better results for a very coarse mesh.

For triangular meshes, the in-plane behavior of DKT18 should be noted as being the same as the T3C0 element. In fact, the elements are essentially different with respect to their bending behaviors.

When combining the T3 and Q4 elements, the results generally come between a uniform triangular mesh and a quadrangular mesh.