RD-E: 5300 Thermal Analysis
A heat source moved on one plate. Heat exchanged between a heatsource and a plate through contact, also between a plate and theatmosphere (water) through convective flux.
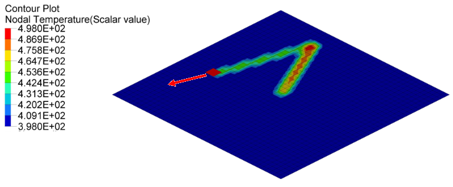 Figure 1.
Figure 1. Options and Keywords Used
- /HEAT/MAT
- /CONVEC
- /IMPTEMP
- /INTER/TYPE7
- /MAT/LAW2 (PLAS_JOHNS)
- Boundary conditions (/BCS)
- Imposed displacement (/IMPDISP)
Input Files
- Heat exchange
- <install_directory>/hwsolvers/demos/radioss/example/53_thermal_analysis/Heat_exchange/*
Model Description
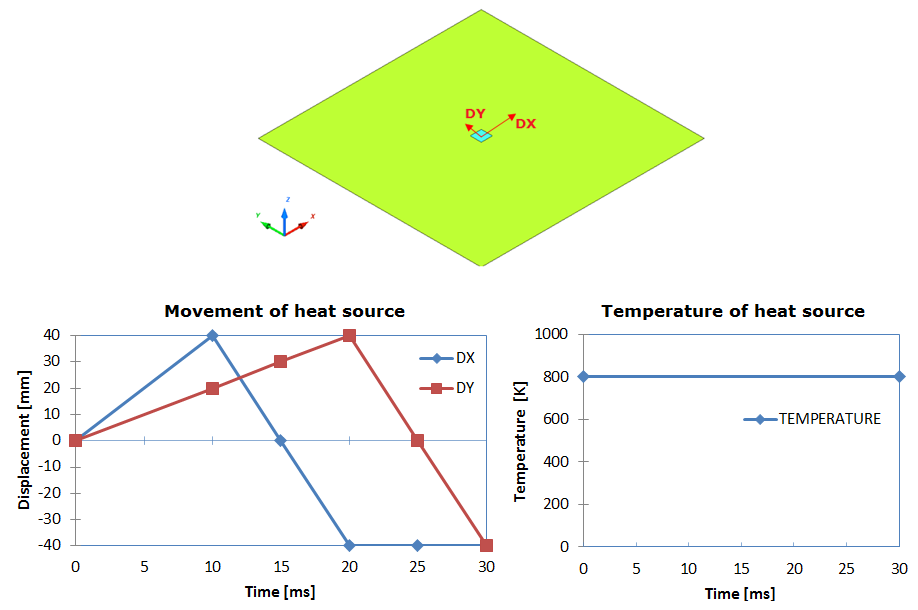
Figure 2. Problem Description
Units: mm, ms, g, N, and MPa
- Material Properties
- Initial density
- 2.8 x 10-3
- Young's modulus
- 70000
- Poisson ratio
- 0.33
- Yield stress
- 206
- Hardening parameter
- 450
- Hardening exponent
- 0.5
- Room temperature
- 298
- Specific heat
- 2.51
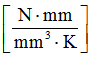
- Initial temperature for heat source
- 800 [K] and for plate: 398 [K]
- Thermal conductivity coefficient AS
- 0.23
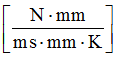
Model Method
/HEAT/MAT is an additional material law card used to describe the material thermal character. So the material ID in the material law in /MAT and in /HEAT/MAT must be the same. The thermal parameter defined in /HEAT/MAT will recover the same parameters which are defined in the material law.
Heat capacity provides heat and mass the ability to change the temperature. In engineering and science, it is recommended to use specific heat capacity, which is heat capacity divided by mass, in SI unit. Heat capacity is for aluminum. Refer to Material Constants in the Theory Manual Appendices for more information on heat capacity of ordinary material.
For the thermal conductivity coefficient AS, . Thermal conductivity for aluminum, and constant thermal conductivity. Set . Since thermal conductivity , then , in this case.
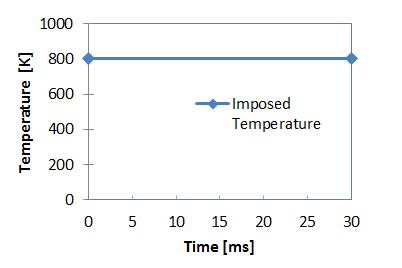
Figure 3. Imposed Temperature for Heat Source
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /CONVEC/convec_ID/unit_ID | |||||||||
| convec_flux_title | |||||||||
| surf_IDT | fct_IDT | sens_ID | |||||||
| Ascalex | Fscaley | Tstart | Tstop | H | |||||
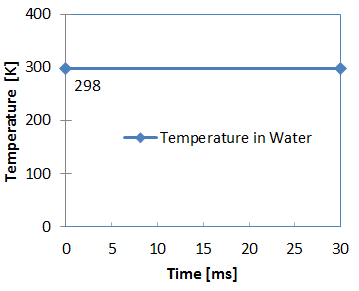
Figure 4. Water Temperature
Where, H is the heat transfer coefficient between structural component and its surrounding infinite room with unit . In general, the convective heat transfer coefficient for water (free convection) is about 20 - 100 and water (forced convection) is about 50 - 10000 . Forced convection in water is .
In /INTER/TYPE7, heat exchange between the heat source and plate during the contact, is defined Kthe=1 to activated heat transfer between main and secondary.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Kthe | fct_IDK | Tint | Ithe_form | AscaleK | |||||
| Frad | Drad | Fheats | Fheatm | ||||||
Ithe_form set to 1 for heat exchange between all pieces in contact.
- Define constant heat exchange coefficient using Kthe ( in SI unit). In this case, fct_IDK = 0.
- If fct_IDK 0, the heat exchange coefficient is the function of contact pressure using this curve and Kthe is the scale factor.
Set Fheats and Fheatm to 0, to not consider heat friction.
Results
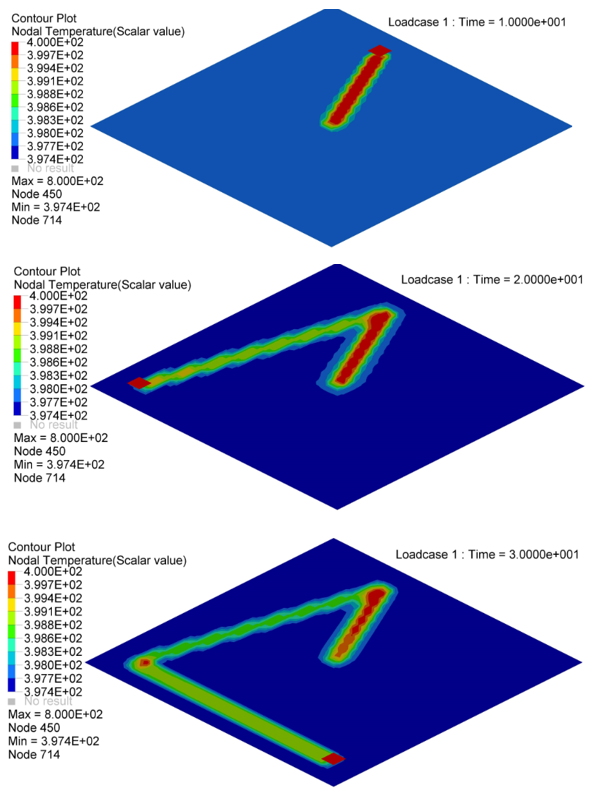
Figure 5. Nodal Temperature in Plate at time=10[ms], 20[ms] and 30[ms]
- Nodal N641 is not under trace. The temperature changed, only due to convection with water.
- Nodal N1034, N958 and N1708 are under trace. At first the temperature
decreased before the heat source began, due to convection with water, and
then increased, due to the heat exchange from the heat source through
contact. Once the heat source is removed, the temperature decreased again,
due to the heat conduction inside the material and convection with water. So
the slope of the temperature decrease is much larger than N641 (only
convection).
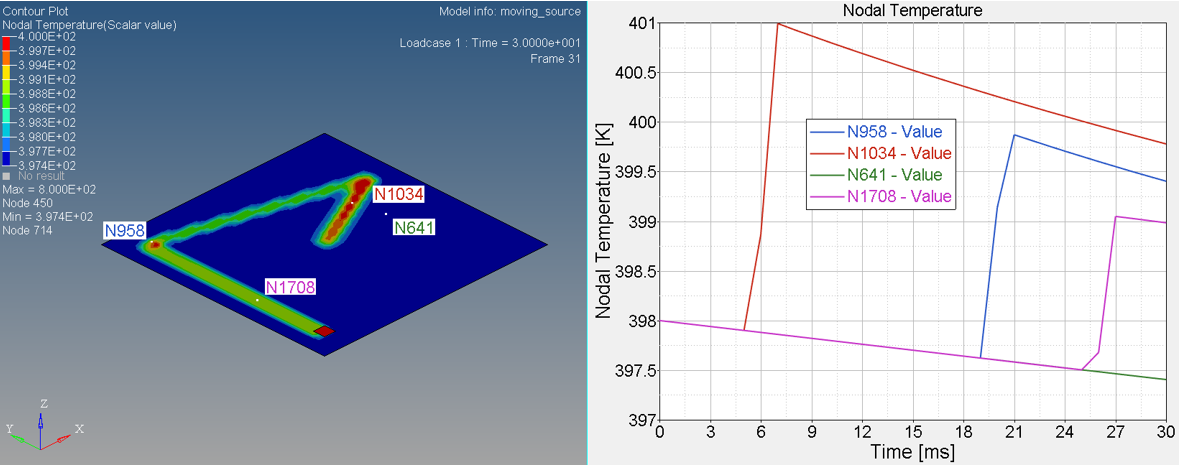
Figure 6. Temperature on Nodal N641, N1034, N958 and N1708