RD-E: 0300 S-Beam Crash

An S-beam is crushed against a rigid wall with initial velocity.

A sensitive study is performed on an S-beam with a crushing load condition. This model uses an elasto-plastic Johnson-Cook material with a penalty based auto-impacting self-contact interface to model the buckling of the beam. An initial velocity is applied on the left section via a kinematic condition with a rigid body. The impacting condition is sliding and modeled using boundary conditions on the right section.

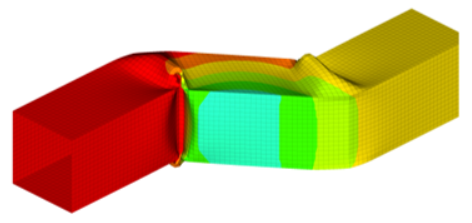
rad_ex3_s-beam
Figure 1.
Three different parameters are varied and results compared:
  • Shell element formulations
    • BATOZ: Ishell=12
    • QEPH: Ishell=24
    • Q4 Belytschko: Ishell=3
  • Global integration versus 5 integration points in shell element
  • Influence of the initial velocity (5 m/s and 10 m/s)
The following criteria is used to compare results:
  • Deformation configuration
  • Crushing force
  • Computation cost
  • Kinetic energy
  • Internal energy

Options and Keywords Used

Input Files

The input files used in this example include:
QEPH
<install_directory>/hwsolvers/demos/radioss/example/03_S-Beam/v_5ms/*
BATOZ
<install_directory>/hwsolvers/demos/radioss/example/03_S-Beam/global_IP/*
BT_type3
<install_directory>/hwsolvers/demos/radioss/example/03_S-Beam/v_10ms/*

Model Description

An S-beam is crushed at an initial rate of 5 m/s against a rigid wall. The section is an empty square-shaped tube (each side measuring 80 mm).

The thickness is 1.5 mm. The tube is made of steel, and plasticity is considered, but not failure.

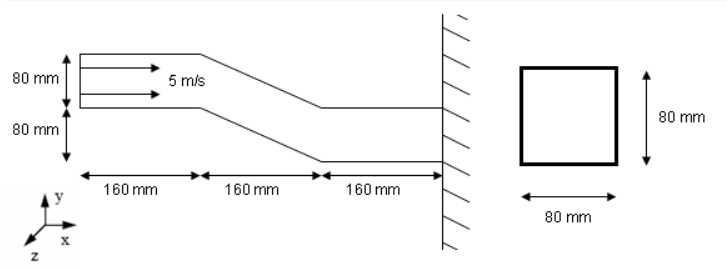
rad_ex_fig_3-1
Figure 2. Problem Description and Beam Cross-section

The mesh is a regular shell mesh. Each shell element measures approximately 5 mm x 5 mm.

The following system is used: mm, ms, g, N, MPa

The material properties used for isotropic elasto-plastic Johnson-Cook law.
Material Properties
Young's modulus
199355 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
Poisson's ratio
0.3
Density
7.9x10-3 [ g m m 3 ] MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaamWaaeaada WcaaqaaiaadEgaaeaacaWGTbGaamyBamaaCaaaleqabaGaaG4maaaa aaaakiaawUfacaGLDbaaaaa@3BBC@
Yield stress
185.4 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
Hardening parameter
540 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
Hardening exponent
0.32
Maximum stress
336.6 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@

Simulation Iterations

A sensitive study is performed comparing:
  • Shell element formulations:
    • BATOZ: Ishell=12 fully-integrated shell element, no hourglassing
    • QEPH: Ishell=24 Reduced integration element with physical hourglass stabilization
    • Q4 Belytschko: Ishell=3 Reduced integration element with elasto-plastic hourglass with orthogonality
  • Through thickness integration method:
    • Global integration (N=0)
    • 5 integration points (N=5)
  • Influence of the initial velocity:
    • 5 m/s and 10 m/s


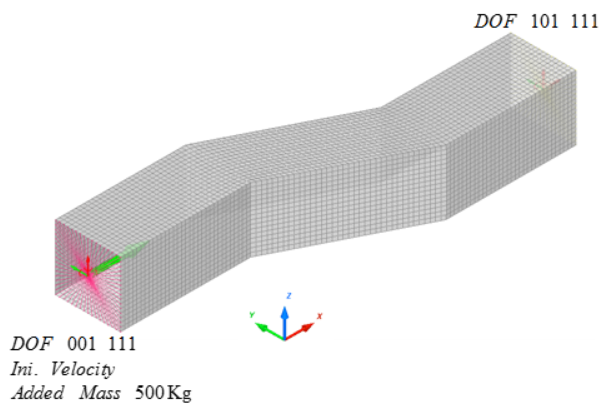
Figure 3. Structure's Overall Mesh

Two rigid bodies were created at the left and right side. Boundary conditions, velocity and added mass are applied on the rigid bodies.

The left section undergoes the following conditions:
  • Fixed in the Z translation, and x, y, z rotation
  • Initial velocity of 5 m/s in the X direction
  • A 500 Kg mass is added on the left end to the rigid body

Results


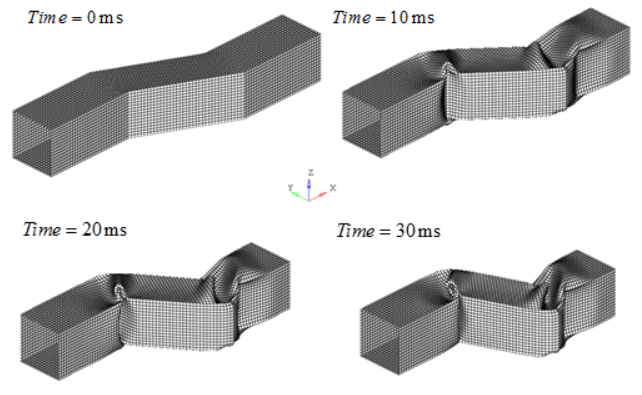
rad_ex_fig_3-4
Figure 4. Deformed Mesh for QEPH Formulation. (N=5, V=5 m/s)

Influence of Different Shell Formulation with N=5

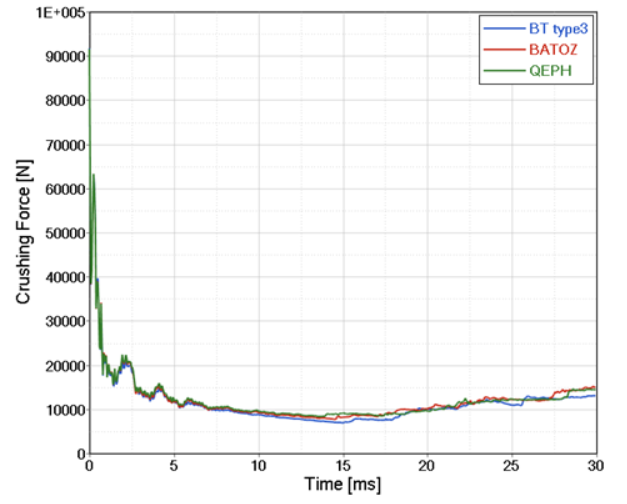
The different shell element formulation only slightly changes the crushing force. The plastic strain results are also similar for these three shell element formulations. Looking at computational cost, the QEPH element is 3 times faster than the fully-integrated BATOZ element. The Q4 TYPE3 Belytschko element is 1/3 times faster than the QEPH, but the Q4 BT TYPE3 element is more susceptible to hourglassing, so QEPH is normally recommended.


Figure 5. Crushing Force versus Displacement DX for Different Shell Formulations. (N=5, V=5 m/s)


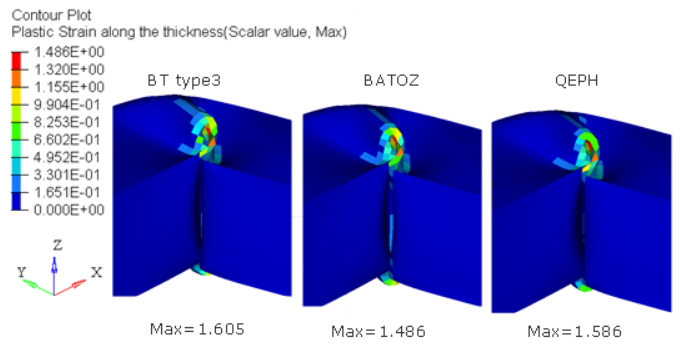
Figure 6. Plastic Strain for Different Shell Formulation. (N=5, V=5m/s)

Influence of Different Integration Points

Table 1 shows that the maximum plastic strain for all elements with global integration (N=0) returns results too low when compared to 5 integration points through the thickness (N=5). When calculating material plasticity through the thickness, using more integration points will increase the accuracy but is computationally more expensive. In general, N=5 is considered a good compromise between computational speed and accuracy. Although using global integration may speed up the computation, it is only compatible with Material Laws 1, 2, 22, 36, 43 and 60 and cannot be used with the failure models (/FAIL) . For additional information, refer to the FAQ Materials/Failure.
Table 1. Computation Cost for Global Integration (N=0), N=3, and N=5
  1 CPU

[normalized]

 Max plastic strain
BT TYPE3

(Ishell=3)

 N=0 0.41 0.981
N=3 0.56 1.596
N=5 0.73 1.605
BATOZ

(Ishell=12)

 N=0 1.78 1.054
N=3 2.53 1.471
N=5 3.24 1.486
QEPH

(Ishell=24)

 N=0 0.65 0.958
N=3 0.78 1.516
N=5 1.00 1.586


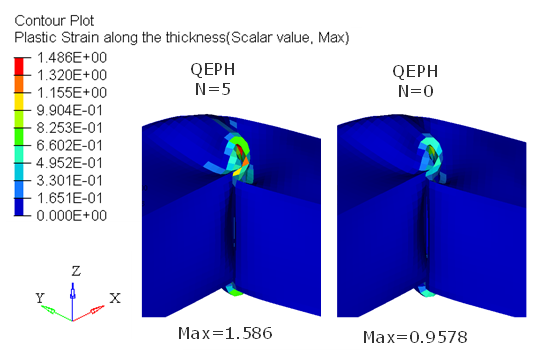
Figure 7. Plastic Strain of QEPH for N=0 and N=5

Initial Velocity Influence

Figure 8 show the influence of the crushing velocity (5 m/s and 10 m/s). This example uses the QEPH shell formulation (Ishell=24) with 5 integration points (N=5).

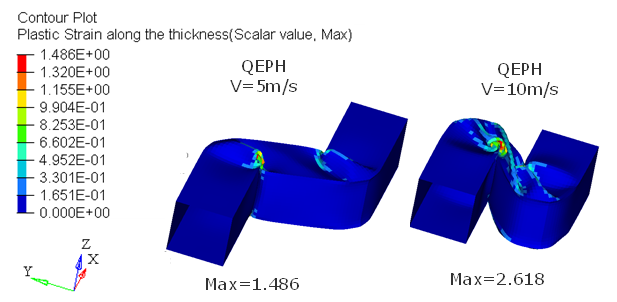
The higher initial velocity gives a larger initial kinematic energy which leads to more deformation and absorbed energy in the beam.


Figure 8. Deformation for the Different Initial Velocities
Table 2. Energy for the Different Velocities
Internal Energy IE

[mJ]

 Kinematic Energy

[mJ]
V=5 m/s 1.674E+6

(factor 1.0)

 4.574E+6

(factor 1.0)
V=10 m/s 4.443E+6

(factor 2.654)

 2.056E+7

(factor 4.495)


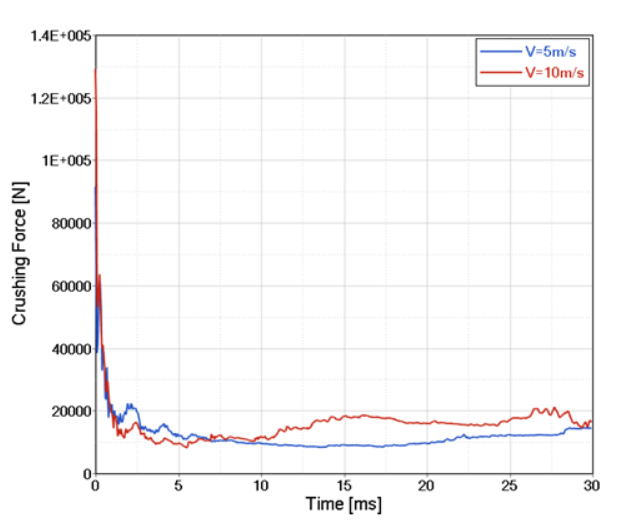
Figure 9. Crushing Force versus Displacement for the Different Initial Velocities

Conclusion

The BATOZ (Ishell=12) and QEPH (Ishell=24) element formulations provide accurate results. Although the Q4 Belytschko (Ishell=3) element is faster, there is always the possibility of hourglassing as shown in RD-E: 0100 Twisted Beam Example. Although more expensive than the Q4 Belytschko element, the QEPH element does not have the hourglassing issue and provides results that are very similar to the more expensive fully-integrated BATOZ element.

Using global integration (N=0) is faster but not as accurate as using N=5 integration points. The global integration results show an under-estimation of the plastic strain and can only be used with a limited number of material laws.