ACU-T：3101 ミキシングエルボにおける過渡共役熱伝達

このチュートリアルでは、ミキシングエルボにおける共役熱伝達を伴う３次元乱流の設定、解析、および結果表示について説明します。ここでは、単純な問題を使用してAcuSolveツールセットを紹介することを目的としています。

CFDシミュレーションの基本的な手順については、ACU-T：2000 ミキシングエルボ内の乱流をご参照ください。この問題の定常シミュレーションのための設定の詳細は、ACU-T：3100 ミキシングエルボにおける共役熱伝達で示されています。このチュートリアルでは、AcuSolveの以下の追加機能を紹介します。
  • 過渡流れのシミュレーション
  • Multiplier Functionの作成と適用
  • 再始動機能の使用
  • 流れシミュレーションと温度シミュレーションの分離（熱シミュレーションのための“凍結”流れ場）
  • 過渡計算結果からのアニメーションの作成

前提条件

入門チュートリアルであるACU-T：2000 ミキシングエルボ内の乱流をすでに完了している必要があります。ここでは、AcuConsole、AcuSolve、およびAcuFieldViewをある程度使い慣れていることを前提としています。ライセンス供与済みバージョンのAcuSolveにアクセスできることも必要です。

このチュートリアルを実行する前に、AcuConsole_tutorial_inputs.zipを<<Altair_installation_directory>\hwcfdsolvers\acusolve\win64\model_files\tutorials\AcuSolveから作業ディレクトリにコピーします。 MixingElbow_ColdSlug.acs をAcuConsole_tutorial_inputs.zipから取り出します。

問題の解析

CFDシミュレーションにおける重要な最初のステップは、解析対象となる工学的な問題を調べ、AcuSolveに対して指定する必要のある設定を決定することです。設定は、形状コンポーネント（ボリューム、入口、出口、壁など）に基づいて行うことができるとともに、流れの条件（流体の物性、速度、流れを乱流または層流のどちらでモデル化するのかなど）に基づいて行うことができます。

問題は、定常状態解と非定常解という２つの構成部分に分けられます。定常シミュレーションにおいて確立された流れ場と温度場は、非定常解析の開始点として使用されます。これらの“凍結”流れ場と温度場の使用により、熱過渡モデルの解析に必要な全体的な解析時間が大幅に短縮されます。流れ場とは別に温度を解析する手法は、幅広い種類の問題に適用できる強力な機能です。このシミュレーションの手法は、温度場と運動量場の分離に依存するということに注意してください。流れ場と温度場との間に強力なつながりがある場合（つまり、温度依存の材料プロパティを介したつながりがある場合）、この手法は適用できません。

定常状態コンポーネントの解析

問題の定常状態部分を 図 1で概略的に示します。これは、ステンレス鋼製のミキシングエルボで構成されており、水が２つの入口から異なる速度と温度で流入します。

このケースは、ACU-T：3100 ミキシングエルボにおける共役熱伝達で使用されたものと同じです。形状は管のXY中央平面に関して対称です（図を参照）。この対称性により、対称面を使用して流れをモデル化することが可能になります。対称面を使用すると、正確な解を維持しつつ、計算時間が短縮できます。



図 1. ステンレス鋼壁のミキシングエルボの概略図

この問題の特性の詳細が、AcuSolveのケースの設定前に作成されたサンプルワークシートから抽出された以下のイメージに示されています。

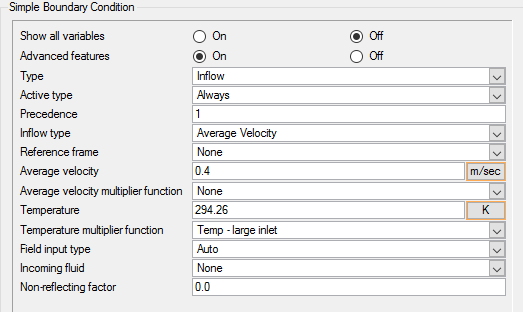
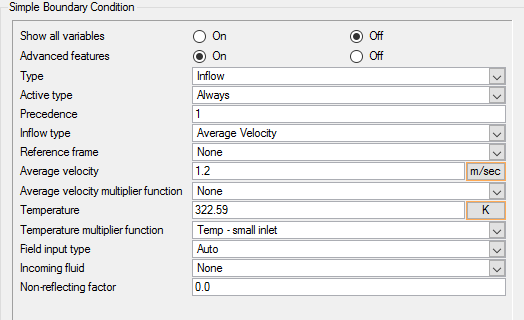
大きい入口の直径は0.1m、入口速度（v）は0.4m/s、流入する流体の温度（T）は295Kです。小さい入口の直径は0.025m、入口速度は1.2m/s、流入する流体の温度は320Kです。管壁の板厚は0.005mです。



図 2.

この問題で扱う流体は水であり、この水の特性は、密度（ρ）が1000kg/m3、分子粘性（μ）が1.0 x 10-3kg/m-sec、伝導率（k）が0.598W/m-K、比熱（cp）が4183J/kg-Kであり（ワークシートを参照）、これらの特性は温度によって変化しません。



図 3.

管壁は、密度が8030kg/m3、伝導率が16.2W/m-K、および比熱が500J/kg-Kのステンレス鋼で作られています。



図 4.

質量保存に基づいて、複合流速（Q）によって、小さい入口の下流に0.475m/sという速度が生じます。この値はレイノルズ数を決定するのに役立ち、さらにこのレイノルズ数を使用して、流れを乱流または層流のどちらとしてモデル化すればよいかを決定できます。



図 5.
モデル化された流れが乱流または層流のどちらになるのかを特定するには、レイノルズ数（Re）を計算する必要があります。レイノルズ数は次の式によって求められます。 (1) Re = ρ V D μ MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciOuaiaacw gacqGH9aqpdaWcaaqaaiabeg8aYjaadAfacaWGebaabaGaeqiVd0ga aaaa@3DE7@ ここで、ρは流体密度、vは流体速度、Dは流れ領域の直径、μは流体の分子粘性です。レイノルズ数が4,000より大きい場合は、一般に流れを乱流としてモデル化することができます。

大きい入口のレイノルズ数が40,000、小さい入口のレイノルズ数が30,000、複合流のレイノルズ数が47,500であることは、流れ領域全体にわたって流れが乱流であることを示します。



図 6.

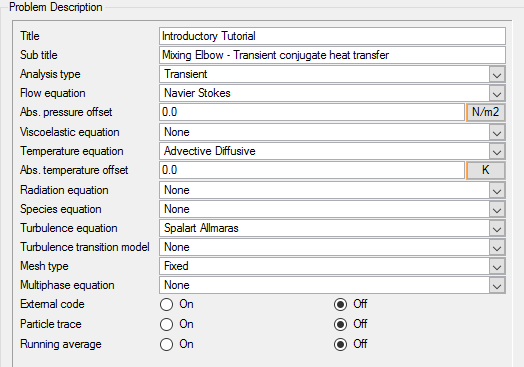
このシミュレーションは、定常状態の乱流をモデル化するように設定されます。また、流れの熱特性は、移流方程式と拡散方程式を使用してモデル化されます。

このシミュレーションは、定常状態の乱流をモデル化するように設定されます。また、流れの熱特性は、移流方程式と拡散方程式を使用してモデル化されます。このシミュレーションは、温度が変化する定常状態の乱流をモデル化するように設定されます。

図 7.

シミュレーションの物理特性を捕捉するための適切な条件を設定することに加えて、優れた結果が得られるように十分に細分化されたメッシュを生成することが重要です。このチュートリアルでは、大きい入口の円周の周りに３０個以上のメッシュ要素が得られるように、グローバルメッシュサイズが設定されます。この問題では、グローバルメッシュサイズは0.0106mです。このメッシュサイズは、モデルの処理時間が短くなるように選択されました。現実のシミュレーションでは、最初の解を得た後、メッシュに依存しない解（メッシュをさらに細分化しても変化しない解）に達するまで、メッシュ設定を変更します。

AcuSolveを使用すると、形状コンポーネント（ボリューム、モデルサーフェス、エッジなど）に依存しないユーザー定義領域内のメッシュ細分化が可能になります。圧力、速度、渦粘性などの勾配が急な領域でメッシュを細分化するのに便利です。この問題では、側管から大きい管に流入する流れによって、解析する必要のある大きな速度勾配が生じます。Mesh refinement zoneを使用して、この領域の流れが捕捉されます。



図 8.

定常状態解を計算した後は、過渡データベースを作成し、設定を変更して、過渡温度特性を解析します。

過渡コンポーネントの解析

問題の過渡部分の開始点を図 9で概略的に示します。これは、流れおよび温度の定常状態解を持つミキシングエルボで構成されます。低温の塊りが、シミュレーション中に両方の入口に注入されます。温度設定により、両方の入口での温度は1.0秒間で283.15Kまで低下します。



図 9. ミキシングエルボの初期状態の概略図

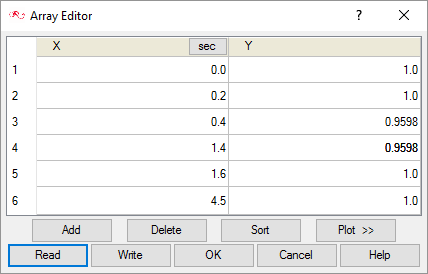
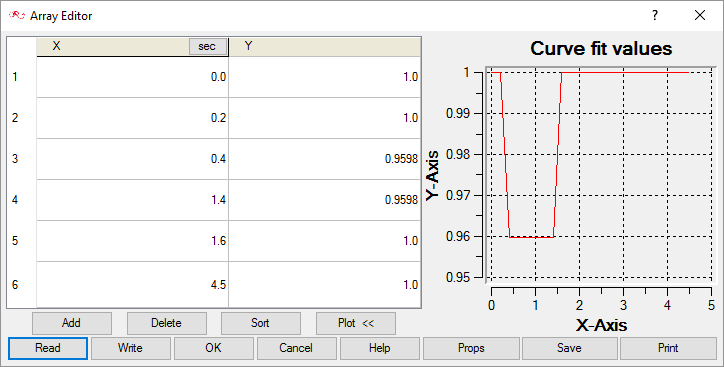
入口での温度プロファイルを図 10に示します。t=0で大きい入口に流れ込む水の温度は295Kであり、t=0で小さい入口に流れ込む流体の温度は320Kです。温度は0.2秒間一定に保たれた後、両方の入口で低下し、0.4秒で283.15K に達してシミュレーションに入ります。温度は1秒間一定に保たれます。1.4秒から上昇し、1.6 秒までに入口温度が初期状態に戻ります。



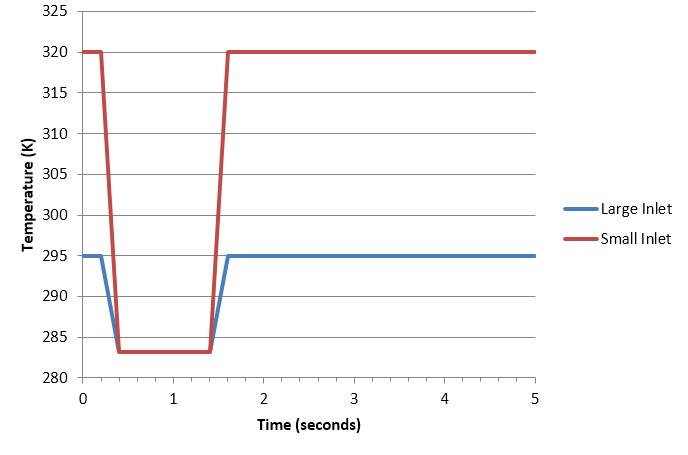
図 10. 入口での過渡温度プロファイル

このケースでは、最小時間は、低温の塊り（以下、コールドスラッグと称す）が領域を完全に通過するのにかかる時間となります。この最小期間は、コールドスラッグの持続時間に、領域を通る定常状態通過時間を加えることで求められます。

通過時間は、大きい入口での入口速度、および流路の推定長を使用して予測できます。流路は長さ0.2mの直線部分（l1）、平均半径が0.15mの90度のエルボ部分（lelbow）、および長さ0.2mのもう１つの直線部分（l2）で構成されています。



図 11.

大きい入口の入口速度は0.4m/秒です。流路が0.6356mだと仮定すると、通過時間は約1.6秒となります。領域を通るコールドスラッグの動きを予測するには、シミュレーション期間は少なくとも3.2秒となります。



図 12.

温度状態が定常状態に戻る時間を考慮に入れるため、シミュレーション時間を追加することができます。このケースでは、1.3秒が追加され、合計シミュレーション期間は4.5秒になります。



図 13.

非定常解析において極めて重要なもう１つの決定事項は、時間増分の選択です。時間増分は、シミュレーションの指定された時間ステップにおける時間変化です。対象となる流動特性の変化を捕捉するのに十分な短さで、不要な計算時間がかからない時間増分を選択することが重要です。

適切な時間増分を決定するために使用される一般的な方法は２つあります。１つ目の方法では、対象となる過渡的挙動の時間スケールを特定し、そのような挙動を十分に解像する時間増分を設定します。２つ目の方法では、指定された時間ステップにおいて流れが通過する可能性があるメッシュ要素の数に、限度を設定します。時間ステップごとの通過したメッシュ要素の数の便利な数学的基準が、Courant-Friederichs-Lewy数、すなわちCFL数です。この方法では、メッシュサイズ、流速、および目的のCFL数から時間増分を計算できます。このチュートリアルでは、時間増分は、コールドスラッグのどの部分も指定のステップの範囲内で２つより多くのメッシュ要素を超えて進むことがないように、グローバルメッシュサイズとCFL数2を使用して計算されました。現実的な問題では、対象となるメッシュゾーン内でのメッシュサイズに基づいて計算します。



図 14.

大きい入口での温度変化は295Kから283.15Kまでとなります。小さい入口では、温度は320Kから283.15Kまで変化します。大きい入口の流れの初期温度に対するコールドスラッグの温度の比率は0.9598です。小さい入口の流れの初期温度に対するコールドスラッグの温度の比率は0.8848です。これらの値は、入口での過渡温度をモデル化するMultiplier Functionの作成時に使用されます。



図 15.

非定常解を計算した後、注目する結果は、シミュレーションにおけるその時々の流体および管壁の過渡熱特性です。

解析パラメータの定義

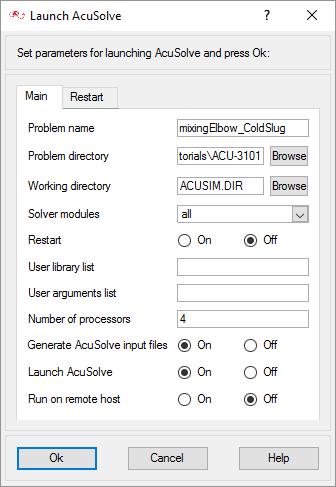
AcuConsoleの起動と定常状態シミュレーションの解析

次の手順では、AcuConsoleを起動し、流れおよび共役熱伝達の定常状態シミュレーションのために設定するデータベースを開きます。その後で、AcuSolveを実行して定常状態解を計算し、AcuFieldViewで結果を表示し、非定常解析のデータベースを保存します。

  1. Windows のスタートメニューからスタート > Altair <バージョン> > AcuConsoleをクリックして AcuConsoleを起動します。
  2. MixingElbow_ColdSlug.acsを開きます。
    1. File > Openをクリックします。
    2. Mixing_Elbow_Cold_Slug\Completed-Steadyを含むディレクトリを参照します。
    3. MixingElbow_ColdSlug.acsを選択し、Openをクリックしてデータベースを開きます。
  3. AcuSolveを実行して定常状態問題を解析します。
    1. ツールバーでをクリックしてLaunch AcuSolveダイアログを開きます。


      図 16.

      これらの設定に基づき、AcuConsoleがAcuSolveの入力ファイルを生成してから、ソルバーを起動します。AcuSolveは、４つのプロセッサ上で実行され、この問題の定常状態解を計算します。

    2. Okをクリックして解析プロセスを開始します。

      メッシング時に、AcuTailウィンドウが開きます。メッシングの進行状況はこのウィンドウで報告されます。メッシングプロセスのサマリーで、メッシュが生成されたことが示されます。



      図 17.

非定常解析データベースの作成

シミュレーションの過渡部分では、定常状態シミュレーションで使用されるのと同じジオメトリおよび同じ多数の属性が使用されます。そのため、定常状態データベースのコピーを作成してから、非定常解析の設定を必要に応じて、その設定を変更することができます。定常と過渡の実行を混同しないよう、非定常用データベースを別のディレクトリに保存します。

以下の手順では、非定常用データベースを作成します。

  1. File > Save Asをクリックします。
  2. １つ上のレベルの..\Mixing_Elbow_Cold_Slugディレクトリを参照します。
  3. File nameとしてmixingElbow_ColdSlugを入力します。
  4. Saveをクリックします。

一般的なシミュレーションパラメータの設定

次の手順では、シミュレーションの過渡部分に必要なグローバル設定を変更します。

非定常解析のために変更する一般的な属性は、サブタイトルおよび解析タイプです。

  1. Data Tree ManagerでBASをクリックして、Data Tree内の基本ビューに切り替えます。


    図 18.
  2. GlobalData Tree項目をダブルクリックして拡張表示します。
    ヒント: 項目名の横にある をクリックしてツリー項目を拡張表示することもできます。


    図 19.
  3. Problem DescriptionをダブルクリックしてProblem Description詳細パネルを開きます。
  4. Sub titleをMixing Elbow - Transient conjugate heat transferに変更します。
  5. Analysis typeをTransientに変更します。


    図 20.

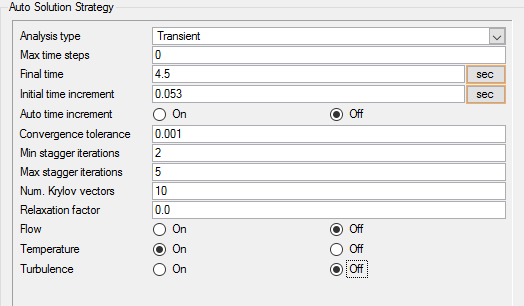
解法パラメータの設定

次の手順では、非定常解析の進行時にAcuSolveの挙動を制御する属性を設定します。



図 21.
  1. Auto Solution StrategyをダブルクリックしてAuto Solution Strategy詳細パネルを開きます。
  2. Max time stepsに0と入力します。
    この値は、AcuSolveでこの設定を無視し、終了時刻および時間増分を使用して時間ステップの最大数を計算する必要があることを示します。
  3. Final timeに4.5と入力します。
  4. Initial time incrementに0.053と入力します。
  5. Min stagger iterationsに2と入力します。
    この設定により、各時間ステップ内で実行される最小反復回数が決定されます。
  6. Max stagger iterationsに5と入力します。
    この設定により、各時間ステップ内で実行される最大反復回数が決定されます。
    最小値2は、収束許容値に達している場合でも、時間ステップごとに少なくとも２回反復が実行されることを表します。最大値5は、収束許容値に達していない場合でも、時間ステップごとに５回までしか反復は実行されないことを表します。５回目の反復までに収束許容値に達した場合、AcuSolveは次の時間ステップに進みます。
  7. Relaxation factorに0と入力します。
    非定常解析を解くときには、緩和係数をゼロに設定する必要があります。緩和係数がゼロ以外だと解の増分更新が起こり、非定常ケースの解の時間精度に影響を与えます。
  8. Flowの横のOffをクリックして流体方程式の求解をオフにします。
  9. Turbulenceの横のOffをクリックして乱流方程式の求解をオフにします。
    これらのオプションをオフにすることで、AcuSolveでこれらの方程式の解が更新されなくなります。代わりに、シミュレーション全体で現在の流れおよび乱流の値（このチュートリアルの定常状態解から生成される）が使用され、AcuSolveでは温度場の解析のみが行われます。


    図 22.

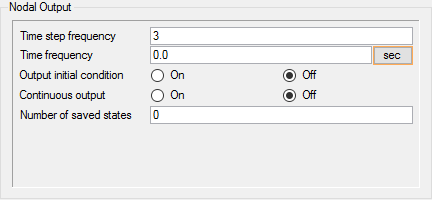
節点出力頻度の設定

次の手順では、非定常解析の結果がディスクに書き込まれる頻度に影響を与える属性を設定します。結果を３つの時間ステップごとに書き込まれた出力状態を使用して、実行の完了後にシミュレーションのアニメーションを作成します。さらに高頻度の出力も使用できますが、その場合はより多くのディスク容量が使用されます。

  1. Data Treeで、Globalの下にあるOutputをダブルクリックして拡張表示します。
  2. Nodal Outputをダブルクリックして、Nodal Output詳細パネルを開きます。
  3. Time step frequencyに3と入力します。
    この値を指定すると、AcuSolveは３つの時間ステップごとに結果を書き込みます。


    図 23.

過渡入口温度のMultiplier Functionの作成

AcuSolveは、シミュレーション中に時間や時間ステップに応じて値を増減させることができる機能を備えています。これは、Multiplier Functionを使用して実現されます。このチュートリアルでは、シミュレーションの進行に伴って入口温度が変化します。Multiplier Functionを利用することで、入口の温度変化をモデル化する関数を簡単に設定できます。

次の手順では、大きい入口での温度のMultiplier Functionを作成し、複製して、そのコピーを小さい入口で使用できるよう変更します。これらのMultiplier Functionは、このチュートリアルで後ほど大きい入口と小さい入口に適用されます。



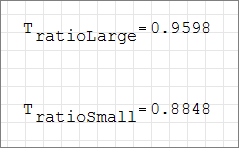
図 24.

このチュートリアルでは、入口温度は初期状態から283.15Kまで低下し、その温度を維持してから、上昇して初期温度に戻ります。



図 25.

Multiplier Functionをできるだけ簡単に作成できるようにするには、Data Tree ManagerでPB*フィルタを使用します。

  1. Data Tree ManagerでPB*をクリックすると、すべての問題定義設定が表示されます。


    図 26.
  2. Data TreeでGlobalの下のMultiplier Functionを右クリックし、Newをクリックして新しいMultiplier Functionを作成します。
  3. Multiplier Functionの名前を変更します。
    1. 新しく作成したMultiplier Function 1を右クリックし、Renameをクリックします。
    2. Temp - large inletと入力し、Enterキーを押します。
  4. Temp - large inletをダブルクリックし、詳細パネルを開きます。
  5. TypeをPiecewise Linearに設定します。
    このオプションは、各時間ステップでMultiplier Functionの値を線形補間するためにAcuSolveで使用される、数値の配列を入力することを示します。この例では、カーブフィットは時間の関数です。


    図 27.
  6. 大きな入口の温度プロファイルにカーブフィット値を追加します。
    1. Open ArrayをクリックしてArray Editorダイアログを開きます。
    2. Addを追加します。
    3. X列に0.2を、Y列に1を入力します。
    4. もう一度Addをクリックし、X列に0.4を、Y列に0.9598を入力します。
      これらのエントリは、シミュレーション中のその時々の温度に対する初期温度の比率を示すために使用されます。
    5. 以下の図に示されているすべての値を入力するまで、この手順を繰り返します。


      図 28.
    6. Plotをクリックし、Array Editorダイアログを拡張表示してカーブフィット値のプロットを表示します。
      プロットを表示するには、右端をドラッグすることでダイアログを拡張表示する必要があります。


      図 29.
    7. OKをクリックします。
  7. Multiplier Functionを複製します。
    1. Temp - large inletを右クリックします。
    2. Duplicateをクリックします。
  8. Copy of Temp - large inletという名前をTemp - small inletに変更します。
  9. 小さい入口用にMultiplier Functionの値を変更します。
    1. Temp - small inletをダブルクリックし、multiplier function詳細パネルを開きます。
      注: Piecewise LinearのTypeは、大きい入口のMultiplier Functionから引き継がれます。
    2. Open ArrayをクリックしてArray Editorダイアログを開きます。
    3. 以下の表に示されている値と一致するよう、Yの値を変更します。
      X（秒） Y
      0.0 1.0
      0.2 1.0
      0.4 0.8848
      1.4 0.8848
      1.6 1.0
      4.5 1.0
    4. OKをクリックします。

過渡入口境界条件の定義

以下の手順では、大きい入口と小さい入口に、時間により温度変化をもたらす入口境界条件を設定します。このためには、このチュートリアルで以前に作成したMultiplier Functionを使用するように境界条件を変更します。

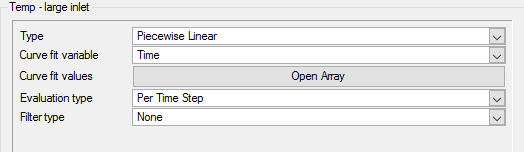
大きい入口の過渡温度の設定

次の手順では、Temp - large inletのMultiplier Functionを大きい入口の境界条件と関連付けます。

  1. Data Tree ManagerでBCをクリックすると、境界条件の設定に関する項目のみを表示します。
  2. Model > Surfaces > Large Inletの順にツリー項目を拡張表示します。
  3. Large Pipeの下にあるSimple Boundary Conditionをダブルクリックして、Simple Boundary Condition詳細パネルを開きます。
  4. Advanced featuresの横のOn をクリックし、その他のオプションを表示します。
  5. Temperature multiplier functionをTemp - large inletに変更します。
    これにより、Multiplier Functionを評価してからその値に指定の温度値を掛けることで温度の入口境界値を決定するようAcuSolveに指示します。乗数関数値が時間に応じて変化するため、入口温度は時間に応じて変化します。


    図 30.

小さい入口の過渡温度の設定

次の手順では、Temp - small inlet Multiplier Functionを小さい入口の境界条件と関連付けます。

  1. Model > Surfaces > Small Inletの順にツリー項目を拡張表示します。
  2. Small Pipeの下にあるSimple Boundary Conditionをダブルクリックして、Simple Boundary Condition詳細パネルを開きます。
  3. Advanced featuresの横のOn をクリックし、その他のオプションを表示します。
  4. Temperature multiplier functionをTemp - small inletに変更します。


    図 31.

解の計算と結果の確認

AcuSolveの実行

次の手順では、非定常解析を実行するためにAcuSolveの設定を変更します。使用する主要機能はリスタートです。リスタートにより、前の解析結果に基づいて解析を開始できます。このケースでは、このチュートリアルにおいて実行した最初の解析の流れ場と温度場が開始点として使用されます。流体方程式および乱流方程式は解法の定義時にはオフだったため、解析されるのは温度場のみとなります。

  1. ツールバーでをクリックしてLaunch AcuSolveダイアログを開きます。
  2. MainタブでRestartの横のOnをクリックします。
  3. Restartタブをクリックします。
  4. From Problemの値がmixingElbow_ColdSlugであることを確認します。
  5. From directoryの横のBrowseをクリックし、定常シミュレーションディレクトリの場所を参照し、ACUSIM.DIRディレクトリを選択します。
  6. 以下の再起動オプションが適切に設定されていることを確認します。
    注: ダイアログを大きくするには、その右端をドラッグします。
    From run 0
    From time step 0
    Reset time step On
    Reset time increment On


    図 32.
  7. Okをクリックして解析プロセスを開始します。

    計算中、AcuTailウィンドウが開きます。解析の進行状況はこのウィンドウで報告されます。解析プロセスのサマリーで、実行が完了したことが示されます。

    このサマリーで提供される情報は、AcuSolveで使用されるプロセッサの数に基づいています。このチュートリアル内で示されている数と異なる数のプロセッサを使用した場合は、示されているサマリーと実行時のサマリーが少し異なる場合があります。



    図 33.
  8. AcuTailウィンドウを閉じ、データベースを保存して設定のバックアップを作成します。

AcuFieldViewでの過渡結果の表示

過渡結果が計算終了したので、AcuFieldViewを使用して流れ場を確認する準備ができました。AcuFieldViewは、AcuSolveに緊密に統合されたサードパーティ製のポスト処理ツールです。AcuFieldViewはAcuConsoleから直接開始できますが、スタートメニューやコマンドラインから開始することもできます。このチュートリアルでは、AcuSolveによって解が計算された後に、AcuConsoleからAcuFieldViewを開始します。

以下の手順では、対称面上の流体と管壁の温度コンターを表示し、ビューに速度ベクトルを追加してから、結果をアニメーション化します。

AcuFieldViewの起動

  1. AcuConsoleツールバーで をクリックしてLaunch AcuFieldViewダイアログを開きます。
  2. OkをクリックしてAcuFieldViewを起動します。
    AcuConsoleからAcuFieldViewを起動するときには、ディスクに書き込まれた、解析の最後の時間ステップの結果が、ポスト処理のために読み込まれます。

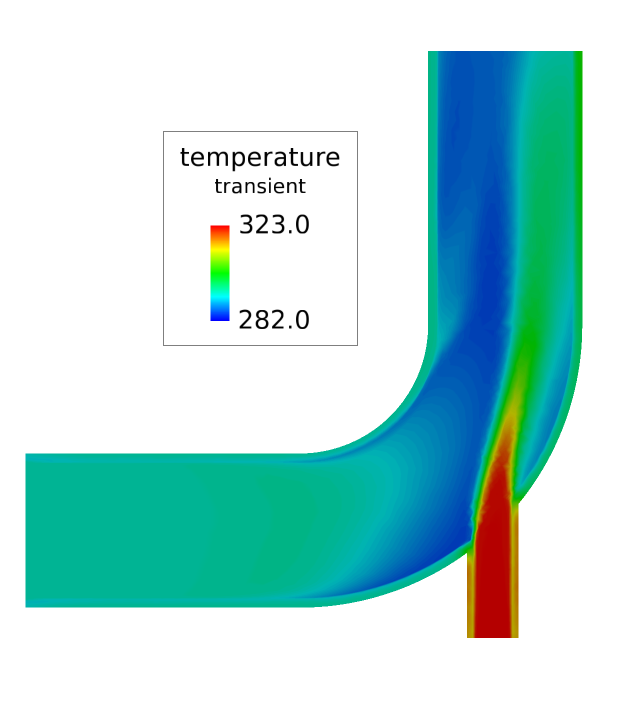
対称面での流体温度および固体温度のコンター表示

次の手順では、境界サーフェスを作成し、非定常解析の最後、中間、および最初に、対称面上での流体温度および固体温度のコンターを表示します。最初の可視化は、シミュレーションにおける最後の時間ステップについてのものであり、AcuFieldViewが起動されたときにAcuSolveから読み込まれる最後の一連の結果です。

  1. をクリックしてBoundary Surfaceダイアログを開きます。
    注: このダイアログはすでに開かれている場合があります。この手順では、このダイアログに焦点を当てます。
  2. Show Meshオプションを無効にします。
  3. 表示するスカラープロパティとしてtemperatureを設定します。
    1. Scalar Functionコントロールグループ内でSelectをクリックし、Function Selectionダイアログを開きます。
    2. リストからtemperatureを選択します。
    3. Calculateをクリックします。
  4. コンター表示用の場所として管の対称面と管壁を設定します。
    1. OSF: Steel Pipe - Symmetryをクリックします。
    2. Shiftキーを押しながらOSF:Symmetryをクリックします。
    3. OKをクリックします。
  5. ツールバーで、Colormapアイコン をクリックします。
  6. Scalar Colormap SpecificationダイアログでBackgroundをクリックし、Whiteを選択します。
  7. ダイアログを閉じます。
  8. シミュレーションで使用する温度の範囲をカバーするようカラーマップを設定します。
    1. Boundary Surfaceダイアログで、Colormapタブをクリックします。
    2. Scalar Coloringの上限値として323を入力します。
    3. Scalar Coloringの下限値として282を入力します。


    図 34.
  9. 凡例Legendをビューに追加します。
    1. Boundary SurfaceダイアログでLegendタブをクリックします。
    2. Show Legendオプションを有効にします。
    3. Frameオプションを有効にします。
    4. ColorグループのGeometricの横にある白の色見本をクリックして、Legend値の色を黒に設定します。
    5. Decimal Placesを1に設定します。
    6. Title欄の横にある白の色見本をクリックして、タイトルの色を黒に設定します。
    7. Subtitleとしてtransientを入力します。
    8. Subtitle欄の横にある白の色見本をクリックして、色を黒に設定します。
    9. Shiftキーを押しながらLegendを左クリックして左側にドラッグすることにより、Legendを移動します。


    図 35.

    このイメージは、白の背景を使用して、遠近法表示とアウトラインをオフにし、表示方向を+Zに設定して作成されました。

    AcuFieldViewが非定常のAcuSolveケースから実行されると、デフォルトで最後の時間ステップからの結果が表示されます。

  10. 非定常解析の中間での温度のコンターを表示します。
    1. ToolsメニューをクリックしてからTransient Dataをクリックし、Transient Data Controlsダイアログを開きます。


      図 36.
      注: Solution Timeの下のスライダーが右端にあることを確認してください。現在表示されているコンターは、シミュレーションの最後からのものです。
    1. スライダーコントロールをTime Step 42まで移動するか、その欄に42と入力し、Applyをクリックします。
      結果として生成されるコンターは、時間ステップ42での温度状態を示します。


      図 37.
  11. 非定常解析の開始時の温度のコンターを表示します。
    1. ToolsメニューをクリックしてからTransient Dataをクリックし、Transient Data Controlsダイアログを開きます。
    2. スライダーコントロールを範囲の最初まで移動し、Applyをクリックします。
      結果として生成されるコンターは、シミュレーション開始時の時間ステップでの温度状態を示します。


      図 38.
    シミュレーション開始時からのコンターがシミュレーション終了時からのコンターと似ていることに注目してください。状態は、コールドスラッグが管を通って広がるにつれて変化してから、初期状態に戻りました。シミュレーションの中間からのコンターは、水と比べた壁の温度変化の遅れを反映し、小さい管の交差位置に近い鋼壁温度が近くの水よりも高いことを示しています。

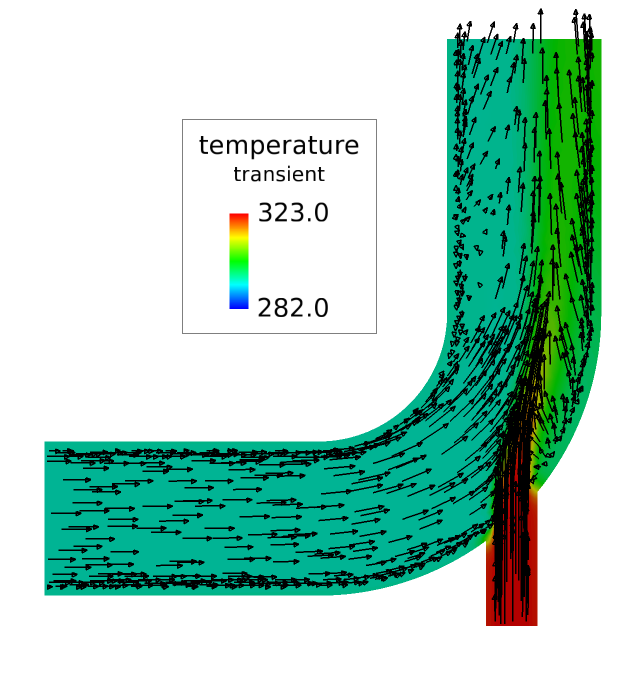
ビューへの速度ベクトルの追加

次の手順では、新しい境界サーフェスを作成して、このサーフェス上に速度ベクトルを表示します。

結果としてもたらされる可視化は、定常状態解のために作成されたものと比較されます。

  1. Boundary SurfaceダイアログのSurfaceタブでCreateをクリックします。
    新しいSurface IDは2になります。
  2. ColoringグループのGeometricラジオボタンをクリックします。
    これにより、ベクトルの色が固定色に設定されます。デフォルトでは、この色は黒です。
  3. ベクトルオプションを設定します。
    1. Vectorsラジオボタンをクリックします。
    2. Vectorsの横にあるOptionsをクリックして、Vector Optionsダイアログを開きます。


      図 39.
    3. Head Scalingを有効にして、2に設定します。
      このオプションによって、ベクトルを基準にした矢印のサイズが決定されます。
    4. Length Scaleを8に設定します。
      この長さスケールによって、ベクトルの長さが決定されます。
    5. Skipオプションを有効にして87.5%に設定します。
      Skipオプションによって、表示を省略するベクトルの比率が決定されます。

      この設定値が37.5%の場合は、62.5%のベクトルが表示されます。

      この設定値が87.5%の場合は、12.5%のベクトルが表示されます。

      この設定値が25%の場合は、75%のベクトルが表示されます。

    6. Closeでダイアログを閉じます。
  4. ベクトル表示用の場所として対称面を設定します。
    1. OSF: SymmetryをBoundary Typesのリストからクリックします。
    2. OKをクリックします。


    図 40.

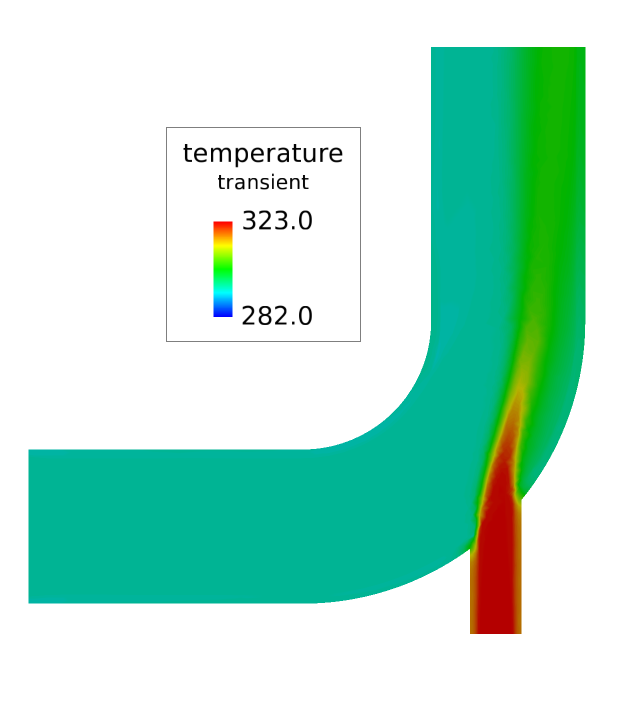
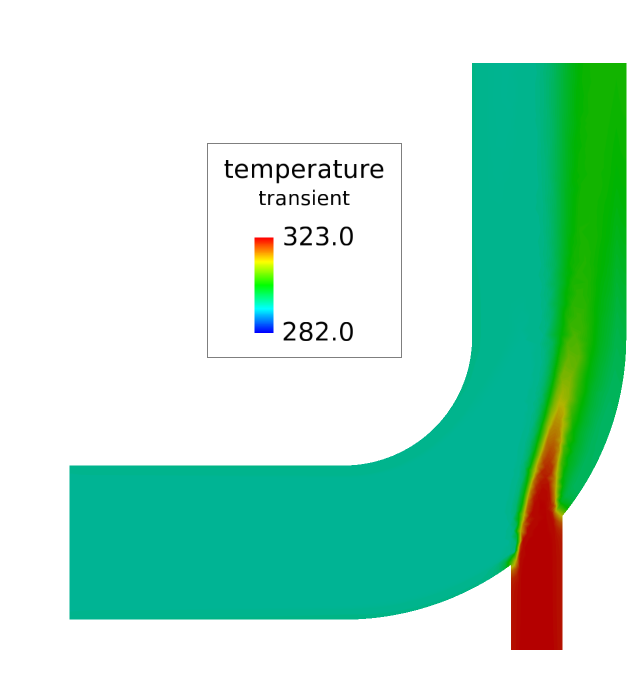
過渡温度のコンター表示

次の手順では、コールドスラッグの過渡熱データを表示します。

  1. 速度ベクトルの表示をオフにします。
    1. Boundary SurfaceダイアログでSurface IDを2に変更します。
    2. Visibilityをクリックしてこのオプションをオフにします。
  2. ToolsメニューをクリックしてからTransient Dataをクリックし、Transient Data Controlsダイアログを開きます。


    図 41.
  3. Sweepをクリックします。
    AcuFieldViewでスイープが準備されると、Transient Data Controlsダイアログで各コントロールが進み、各時間ステップでの可視化の更新が表示されます。スイープが終了しても、コントロールを変更するまで継続的に再生されます。
  4. 再生率を変更します。
    1. Viewメニュー、Minimum Time Between Framesの順にクリックします。


      図 42.
    2. Minimum Time Secondsを0.10に設定します。
    Sweep Controlオプションを使用して、スイープの一時停止、フレームの先送りや前戻し、およびスイープの再生を行います。
  5. Transient Data Controlsダイアログを閉じます。
  6. OKをクリックしてTransient Data Controlsメッセージダイアログを却下します。

過渡温度スイープのアニメーション化

次の手順では、過渡スイープを作成し、AcuFieldViewから独立して表示できるアニメーションとしてこのスイープを保存します。

  1. ToolsメニューをクリックしてからTransient Dataをクリックし、Transient Data Controlsダイアログを開きます。
  2. Tools > Flipbook Build Modeをクリックします。
  3. OKをクリックしてFlipbook Size Warningダイアログを抜けます。
    Transient Data ControlsダイアログのSweepボタンがBuildに変わります。


    図 43.
  4. スライダーコントロールを使用してSolution Timeを最初の時間ステップに設定し、Applyをクリックします。
  5. Buildをクリックします。
    AcuFieldViewでフリップブックアニメーションが作成されるときには、あらかじめTransient Data Controlsダイアログにコントロールが表示されます。フリップブックが作成されると、Flipbook Controlsダイアログでそのアニメーションの再生または保存が可能になります。


    図 44.
  6. をクリックしてアニメーションを再生します。


    図 45.
  7. をクリックして再生を一時停止します。
  8. AcuFieldViewとは独立したムービーを再生可能にするためにフリップブックを保存します。
    1. Saveをクリックします。
    2. ..\Mixing_Elbow_Cold_Slugディレクトリを参照します。
    3. File nameにcold_slugと入力します。
    これで、このアニメーションcold_slug.aviは他のソフトで表示可能になりました。
  9. Flipbook ControlsダイアログをCloseで閉じ、OKをクリックしてFlipbook Exit Confirmation警告を抜けます。

要約

このチュートリアルでは、非定常解析ケースを設定する基本的なワークフローに取り組みました。非定常解析の初期状態として使用する、十分に設定された定常状態ケースが提供されました。非定常解析は、“凍結流”の手法を使用して、速度場を再計算することなく過渡温度場をシミュレートすることで行いました。過渡ケースを設定して解析した後、モデルの対称面に沿ったコンターおよびベクトルのビューの作成、および温度コンターのアニメーション化が可能になるようAcuFieldViewで結果をポスト処理しました。このチュートリアルで紹介した新機能は、非定常解析、Multiplier Function、リスタート、凍結流、過渡結果のアニメーションです。