水力学システムのモデリング

Hydraulics (By Fluidon)ライブラリを使用した水力システムのモデリングについて学習します。

Hydraulics（By Fluidon）

Activateでは、Hydraulics (By Fluidon)ブロックライブラリを介した水力システムのモデリングが可能です。

Hydraulics（By Fluidon）は、流体動力システムの1次元シミュレーションで使用するModelicaライブラリです。Hydraulics（By Fluidon）ライブラリによって作成されたモデルは、集中パラメータ手法に基づいています。このライブラリは、さまざまな水力コンポーネントおよび事前定義された作動液で構成されます。

水力システムの基本的なダイアグラム

Activateで水力システムをモデリングする場合、Hydraulics（By Fluidon）ライブラリに用意された2つのブロックであるLiquidブロックとEnvironmentブロックが必要です。

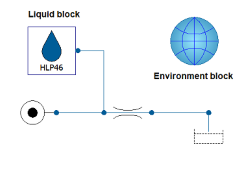
Environmentブロックは、周囲の圧力や重力定数の値のような、環境条件に関する情報を収めています。Liquidブロックは、モデルで使用する作動液を規定します。モデルを構成するすべての水力コンポーネントを、このブロックに接続する必要がある理由は、この点にあります。各コンポーネントにLiquidブロックを手動で容易に接続できるように、一定の範囲のコンポーネントにはforwardFluidPropertiesオプションが用意されています。このオプションを使用すると、流体情報がコンポーネント間で転送されるので、Liquidブロックを各流体回路に一度だけ接続すればすみます。

集中パラメータ手法の基本

水力エンジニアリングの集中パラメータ手法では、水力システム内部の断面の状態を流量と圧力で全面的に記述できることを想定しています。集中パラメータ手法には数値上の制限があることから、一般的にその適用範囲は動的作用が低～中程度のシステムに限られます。インポートされたパラメータ手法は、抵抗器、コンデンサー、インダクターの3つの基本的な水力コンポーネントが関係しています。

抵抗: 抵抗は、慣性や流体剛性がない理想的な損失を表します。その構成式は次のように記述できます。 EquationNumberStart1EquationNumberEnd $\dot{m} \propto Δ p^{n}$
この式によれば、質量流量が、コンポーネント両端の圧力降下のn乗に比例することが想定されています。この指数は、流動様式（層流、乱流、またはこの2つの間で遷移する状態）に応じて、1～0.5の範囲で変化します。

コンデンサ: 抵抗と対照的に、コンデンサは損失や慣性がない理想的な流体ばねに相当します。数学的には、この動作を次の微分方程式で記述できます。EquationNumberStart2EquationNumberEnd $\frac{d p}{d t} = Δ \dot{m} \frac{K}{V}$
このモデルによると、圧力の一時的な変化は、流入側と流出側の質量流量差に各コンポーネントの体積弾性係数を乗算し、その積を各コンポーネント内部の流体密度と流体体積で除算した値に比例します。

インダクタ: インダクタは、損失や剛性のない理想的な慣性です。数学的には次の式で記述できます。 EquationNumberStart3EquationNumberEnd $\frac{d \dot{m}}{d t} = Δ p \frac{A}{L}$
この式は、ニュートンの運動の第2法則にある水力学の公式です。この式によれば、質量流量の一時的な変化は、コンポーネント両端間の圧力差に流れの断面積を乗算し、その積をコンポーネントの長さで除算した値になります。

水力コンポーネントの扱い

抵抗、コンデンサ、インダクタを単独または組み合わせて使用することで、実際の水力システムをモデリングできます。これらのコンポーネントでモデリングしたシステムを回路モデルに接続すると、数値解析の対象となる連成常微分方程式のシステムが形成されます。解析アルゴリズムは収束値の前後を往復するように動作し、初期の圧力分布に基づいて抵抗とインダクタから流量が計算されます。つづいて、これらの流量がコンデンサの境界条件として機能し、その条件に基づいて新しい圧力分布が計算されます。このステップの後、手順全体が繰り返されます。ここで説明したアルゴリズム構造の特性から考えると、合理的な初期圧力を、コンデンサ要素に基づくコンポーネント（簡単な体積など）に割り当てる必要があります。