Friction Formulation
This section provides information about the LuGre and Dahl formulations for friction.
LuGre Model
The LuGre model, which supports both stiction and dynamic friction, is implemented. In the LuGre formulation, a bristle model is used to idealize friction. When a tangential motion arises between the surfaces, the bristles deflect like springs. If the deflection is sufficiently large, the bristles start to slip. A bristle model is used to idealize the friction between two mating surfaces. The slip velocity between the mating surfaces, , determines the average bristle deflection for a steady state motion. It is lower at low velocities, which implies that the steady state deflection decreases with increasing velocity. The figure below depicts the bristle model:
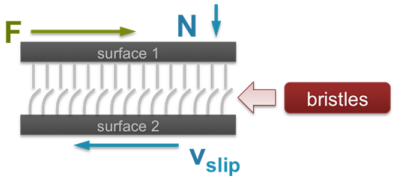
Figure 1.
The LuGre model represents several different effects:
- The effect of the mating surfaces being pushed apart by lubricant.
- The Stribeck effect at very low speed. When partial fluid lubrication exists, contact between the surfaces decreases and thus friction decreases exponentially from stiction.
- Rate dependent friction phenomena such as varying break-away force and frictional lag.
- Static friction between two surfaces.
Define the following quantities:
- Ball radius
- Normal force between a pair of surfaces.
- Coefficient of static friction.
-
Coefficient of dynamic friction (µd ≤ µs).
- True friction torque between the surfaces.
- Constants associated with the LuGre model.
Assuming contact on a spherical surface, the friction force is a 2-dimensional quantity in the friction plane, but a 3-dimensional quantity in the I-Marker coordinate system. Joint friction is calculated using the algorithm shown next:
| Quantity | Formula |
|---|---|
| Angular slip velocity | |
| Bristle states | |
| Stiction to dynamic friction transition function | |
| Coupling function | |
| Rate dependence function | |
| Model for dynamic simulation |
|
| Model for static simulation |
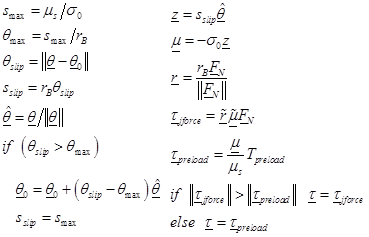 |
The LuGre model supports the notion of a friction ellipse. The term in the above equations, , represents the coupling effect between the friction forces in two orthogonal directions in the friction plane. This coupling effect leads to the familiar friction ellipse that defines the limiting forces when sliding is seen in both orthogonal directions, as shown in the figure below:
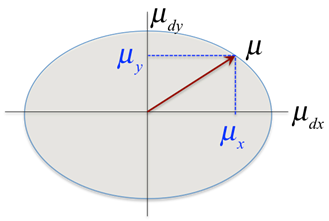
Figure 2.
Dahl Model as a Subset of the LuGre Model
The Dahl model of friction can be obtained from the LuGre model simply by setting the parameters and , as explained in the figure below. The Dahl model does not use the terms shown in red.

Figure 3.
Comparison Between the Dahl and LuGre Models
The Dahl model requires fewer parameters. In the absence of experimental data, one should use the Dahl model. However, the Dahl does not capture many of the effects of the LuGre model. The Dahl model does not support:
- Stribeck effect (also known as the stick-slip effect)
- Static Friction > Dynamic Friction
- Bristle damping
- Memory-less damping (viscous damping)
- Rate dependency (such as dependency of friction force on frequency of input)!
Rate dependency is an important property and is illustrated in the figure below:
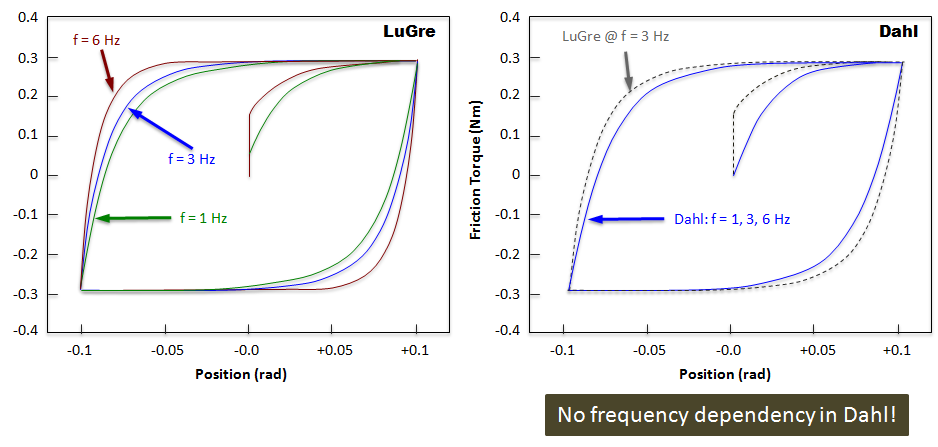
Figure 4.
The curves in the figure represent the hysteresis loop in the friction models that cause energy dissipation. Notice that the LuGre model (left) is sensitive to the frequency of the input. In contrast the Dahl model (right) shows no change in its response even when the frequency of the inputs change.