Weighted Bilinear Interpolation (WBI) Algorithm
This algorithm1 is almost identical to the arithmetic mean (AM) algorithm. The gains and angle distances are also read from the vertical and horizontal pattern and are weighted according to their distances.
In contrast to the bilinear interpolation (BI) algorithm, the vertical angles are additionally weighted with the factor . Therefore, the gain values read from the vertical pattern are no longer relevant in the horizontal plane (for = 90°), and the horizontal pattern is, therefore, more accurate.
The mathematical equation for the computation of the weighted bilinear interpolation is:
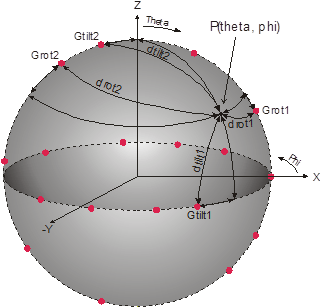
Figure 1. Angles and gains used for the weighted bilinear interpolation.
The weighted bilinear interpolation leads to more accurate results compared to bilinear interpolation (BI) algorithm. The mean error is approximate 1.3 dB and the standard deviation is 0.6 dB for a - dipole.
The most accurate results can be obtained with this algorithm if the main radiation of the antenna is in the horizontal plane.