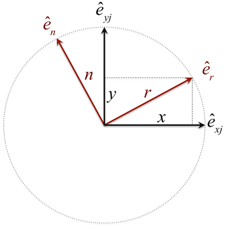
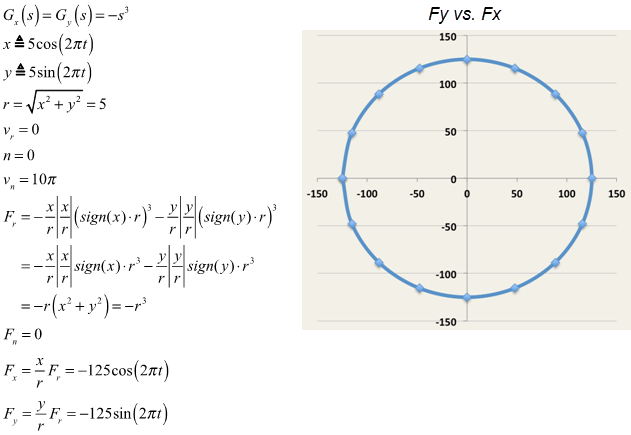
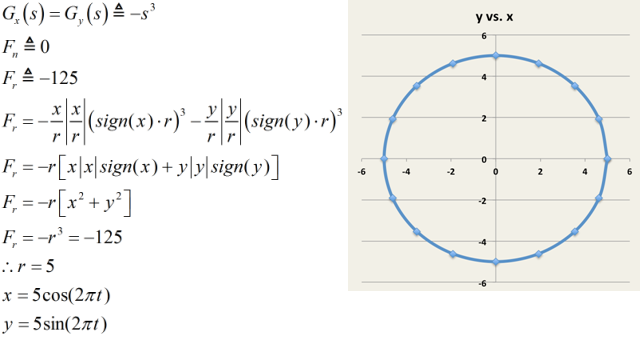
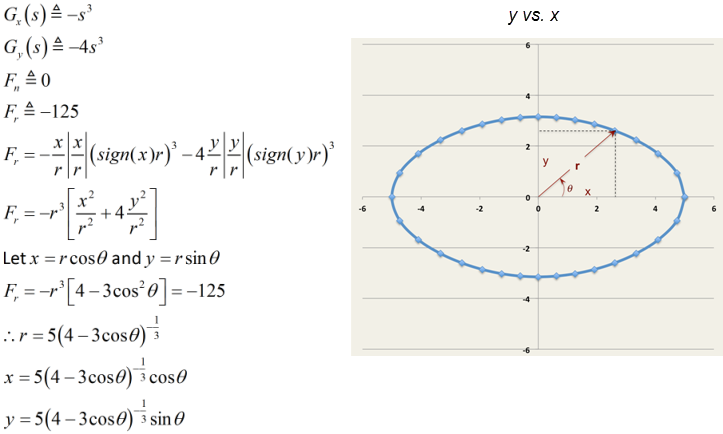
| Deforming vector |
|
| Unit vector along radial deformation |
|
| Unit vector perpendicular to deformation |
|
| Bushing radial deformation |
|
| Bushing tangential deformation |
|
| Deformation velocity vector |
|
| Bushing radial deformation velocity |
|
| Bushing tangential deformation velocity |
|
| Bushing force vector |
|
| Radial force |
|
| Tangential force |
|
| Force in the x-direction |
|
| Force in the y-direction |
|