Sensitivity Analysis
OPTFEKO calculates upon termination of an optimisation, a sensitivity analysis of the goal function with relation to each parameter.
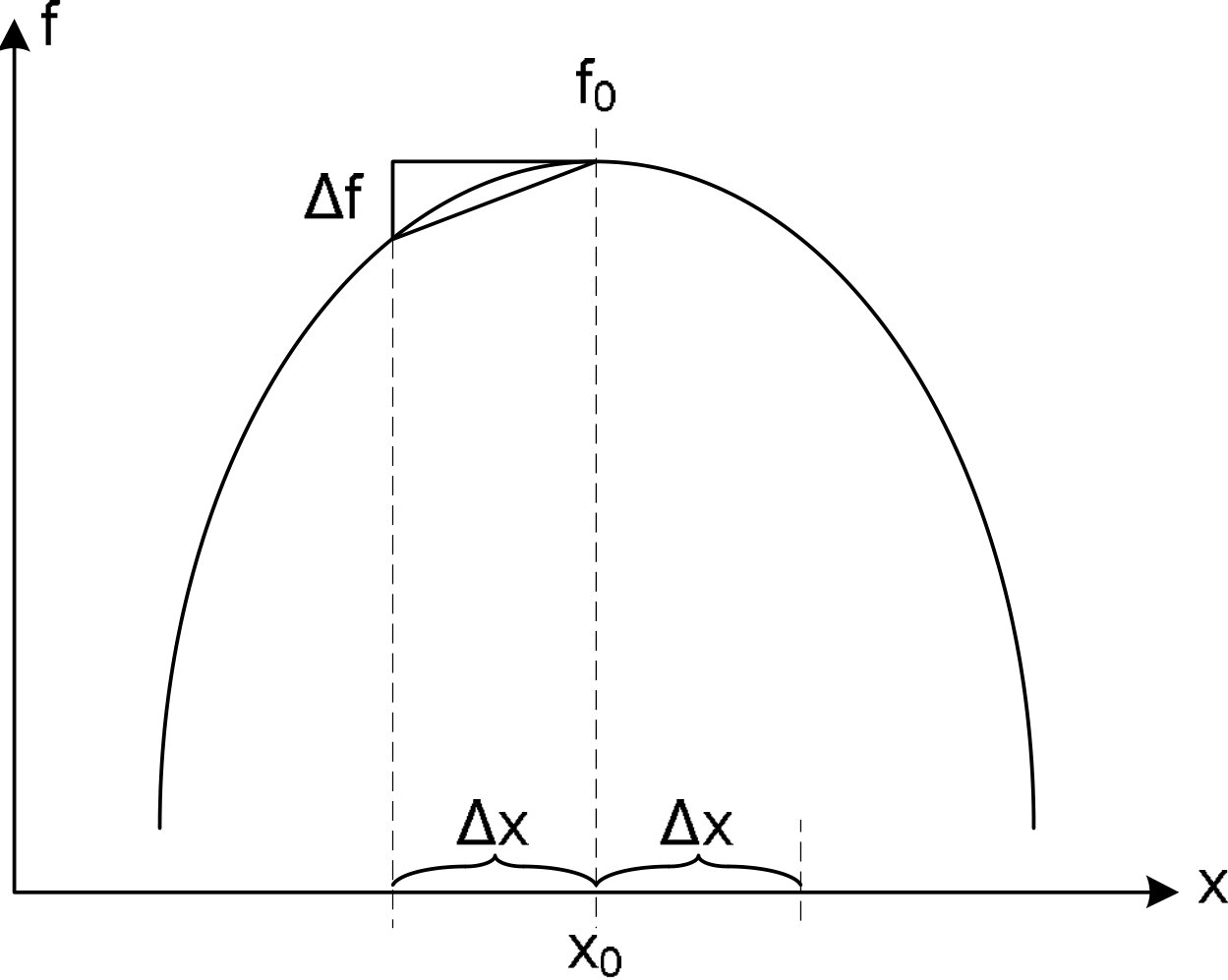
Figure 1. Sensitivity analysis of the goal function f with relation to the parameter x.
Figure 1 shows an example goal function f that varies as a function of the parameter x. The sensitivity with relation to the parameter x can be described by the following equation:
A sensitivity analysis will only be performed if at least 2N +1 samples are available for a problem with N parameters and these samples should all be within a 5% radius of the optimum. If the samples under consideration are scattered outside of a 5% radius of the optimum, the stored data is considered insufficient for proper sensitivity analysis. It should also be realised that as this computation makes use of already computed samples only, the accuracy of the reported sensitivity number depends on how well the algorithm has converged.