Tutorial: Working with Model Hierarchy and Parameterization
Learn how to add a PID controller and dynamics to a water tank model. Learn how to parameterize the model with context variables and mask super blocks to hide details of the model hierarchy.
Files for This Tutorial
Watertank.scm
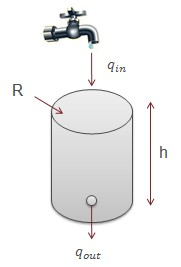
Overview of a Watertank Problem
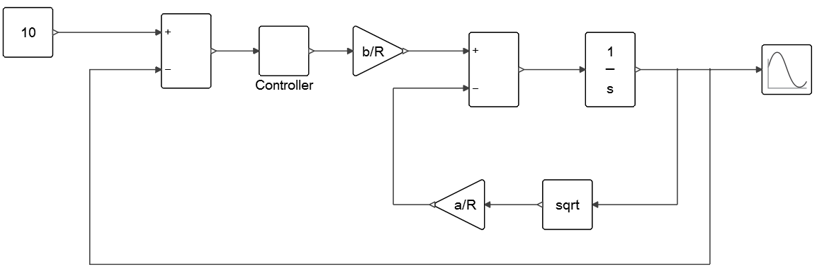
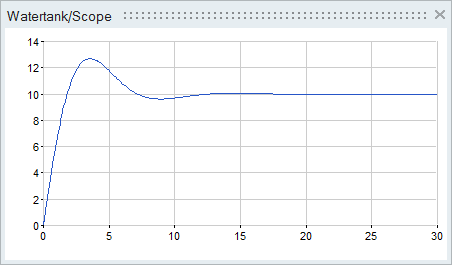
In a water tank model, a PID controller is added to regulate the flow of water into the tank.
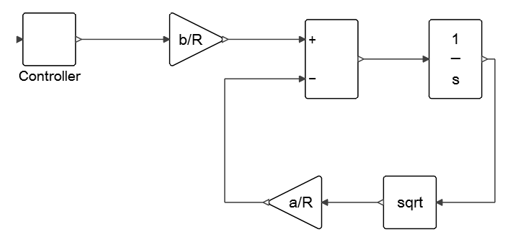
The following flow equations represent the water tank model:
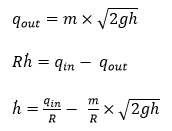
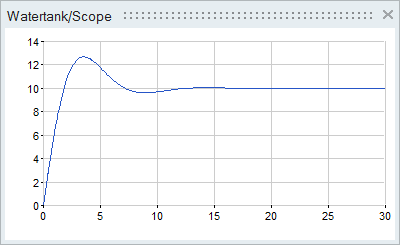
By controlling the inflow rate qin of water into the tank, the water level h can be reached within a given time. The given system model has only one input and one output, qin and qout, and therefore requires the addition of a classic PID controller to control the flow rate of water.
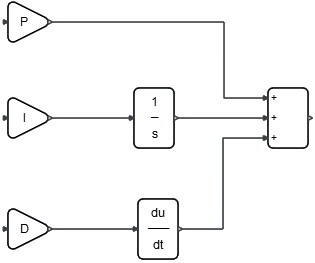
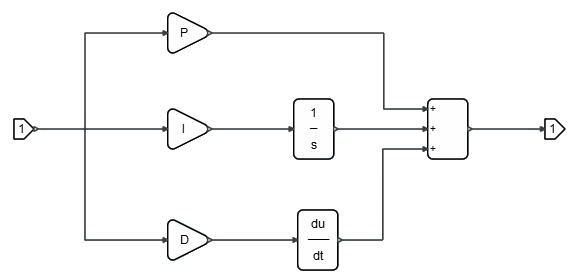
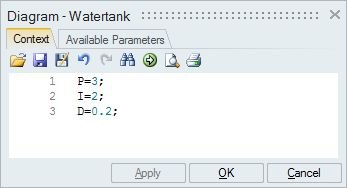
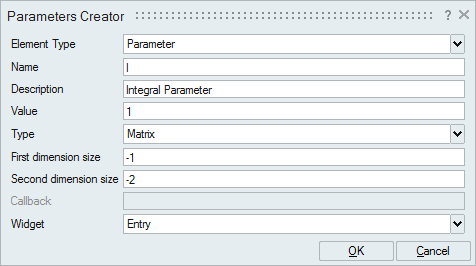
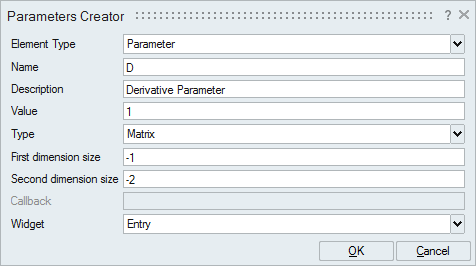
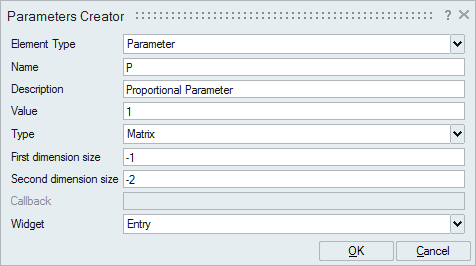
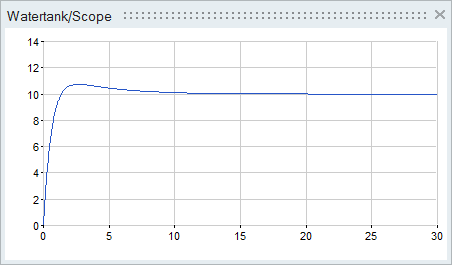
The PID controller is implemented as a super block that is comprised of basic arithmetic and integration blocks. The coefficients of the Proportional, Integral and Derivative terms of the PID controller are defined as context variables, which you can edit with OML commands.
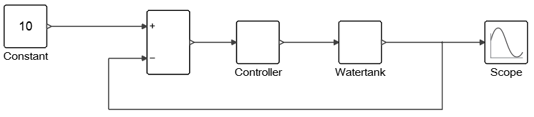
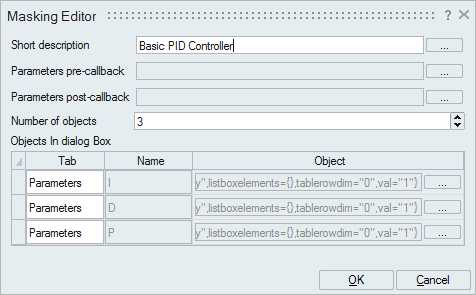
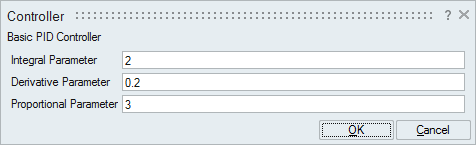
The controller in the super block is masked and looks like a regular Activate block. Though the mask hides the implementation details of the super block, the PID parameters are accessible by double-clicking the super block.
Constructing a PID Controller
Create a model with a PID controller to regulate water flow.
Modeling the Water Tank Dynamics
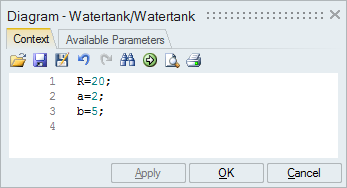
Construct the dynamics of a water tank based on three flow equations.
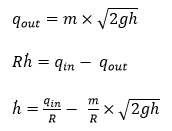
Defining Context Variables
On the Context tab of the Diagram dialog, enter values for the main and local context variables.
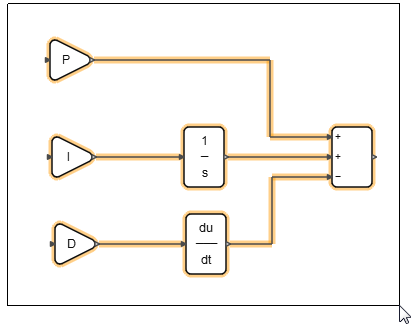
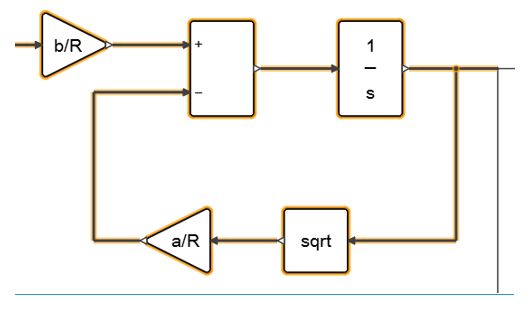
Masking the Super Block
Mask the Controller super block and tune the P, I, and D parameters.