mscohere
Estimates the mean squared coherence of time domain signals.
Syntax
msc=mscohere(x,y)
msc=mscohere(x,y,window)
msc=mscohere(x,y,window,overlap)
msc=mscohere(x,y,window,overlap,nfft)
msc=mscohere(x,y,window,overlap,nfft,fs)
msc=mscohere(x,y,window,overlap,nfft,fs,range)
[msc,freq]=mscohere(...)
Inputs
- x
- The signal.
- window
- The window size, or the window vector.
- overlap
- The number of overlapping points in adjacent windows.
- nfft
- The size of the fft.
- fs
- The sampling frequency.
- range
- The spectrum type: 'onesided' or 'twosided'.
Outputs
- msc
- The mean squared coherence.
- freq
- The vector of frequencies corresponding to the coherence values.
Example
Coherence of two signals sharing common frequency components.
n = 4096;
fs = 256;
ts = 1/fs;
t = [0:ts:(n-1)*ts];
w1 = 2*pi*20;
w2 = 2*pi*32;
w3 = 2*pi*48;
w4 = 2*pi*60;
signal1 = 5*cos(w1*t) + 7*cos(w2*t) + 3*cos(w4*t);
signal2 = 7*cos(w1*t + (pi/2)) + 5*sin(w3*t) + 2*cos(w4*t + pi);
rand('seed', 2019);
signal1 = signal1 + randn(1, n);
signal2 = signal2 + randn(1, n);
window = ones(1, 64);
mscohere(signal1, signal2, window, 0, [], fs);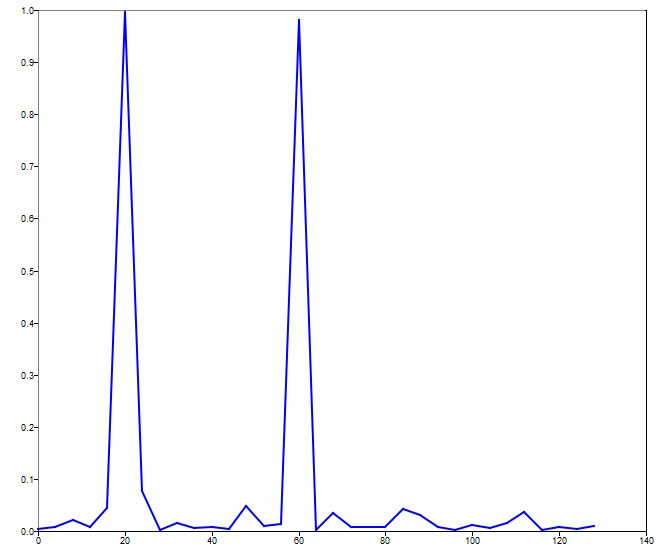
Figure 1. impz figure 1
Comments
With no return arguments, the function will automatically plot.
It is often recommended to remove the signal means prior to calling mscohere. The function does not remove the mean automatically.
- window
- A Hamming window with the largest length that produces eight data segments.
- overlap
- One half of the window length.
- nfft
- The window length. A larger value will pad zeros to each block of windowed data.
- fs
- 1.0 Hz.
- range
- 'onesided'