RD-V: 0020 Cantilever Beam
Deflection of a cantilever beam modeled with different meshes and different element formulations.
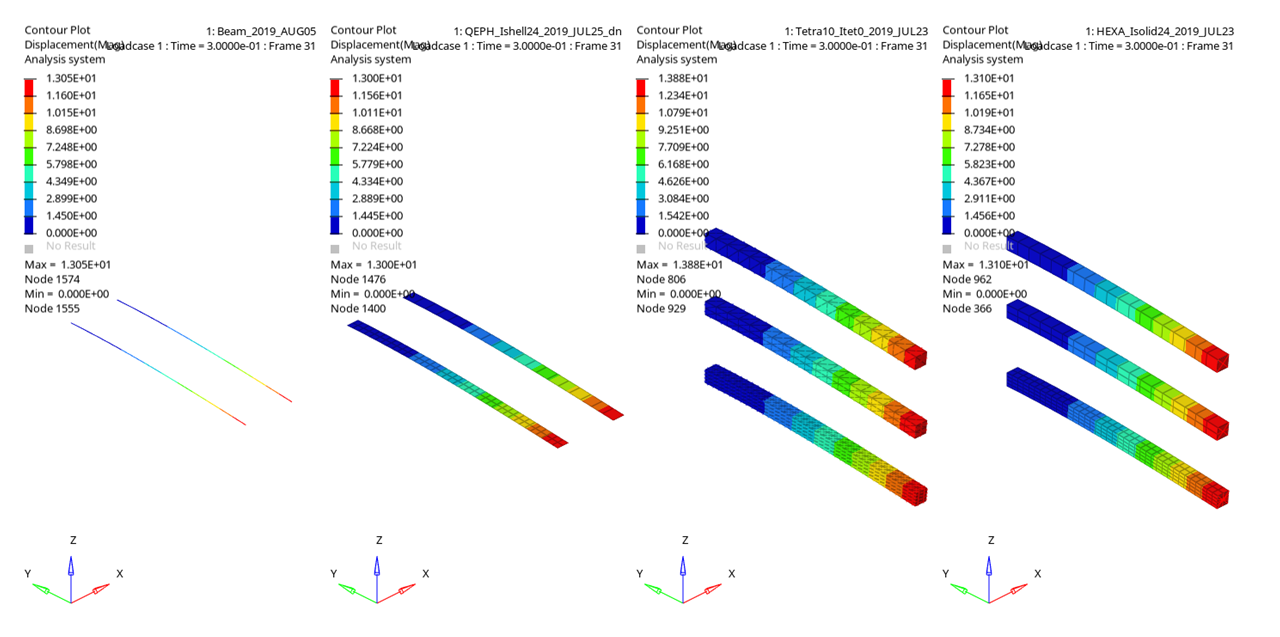
Figure 1.
The subject of this study is to analyze the quality of Radioss quasi-linear simulation using a simple use case. This should give an overview about the trade-off between quality and performance with respect to different modelling techniques. This example deals with the use of Radioss nonlinear solver.
Based on a well-known from literature small example, the set-up of a simple Radioss input deck for the linear-elastic application will be shown: the cantilever-beam.
The beam is clamped on one side and loaded with a concentrated force on the other side. The maximum deflection is used for results comparison. This problem is well known, and results can be easily compared with an analytical solution.
In this example, different mesh techniques are compared: beams, shells, hexahedron elements and tetrahedron (tetra4 and tetra10) elements, as well as different element sizes.
The results are extracted and compared between each other with respect to their mesh size and element formulation. As output, the maximum deflection, number of cycles, calculation time, element stress, and overall error are used. The maximum deflection is compared to the theoretical value.
Options and Keywords Used
- /PROP/TYPE1 (SHELL)
- /PROP/TYPE3 (BEAM)
- /PROP/TYPE14 (SOLID)
- /TETRA4
- /TETRA10
- /BEAM
- /BRICK
- /SHELL
- /CLOAD
- /ADYREL
- Mesh density
Input Files
The following input file is used in this verification problem:
<install_directory>/hwsolvers/demos/radioss/verification/elements/0020_beam/
Model Description
This example's purpose is to compare different modeling methods for a simple cantilever beam in terms of quality and performance.
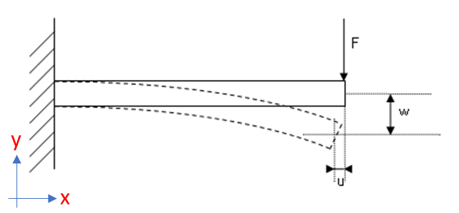
Figure 2. Cantilever Beam with Single Load at the Beam End
- Initial density
- 7.8 x 10-9 [Mg/mm3]
- Young's modulus
- 210000 [MPa]
- Poisson ratio
- 0.3
- Thickness
- 10 [mm]
- Length
- 190 [mm]
- Width
- 10 [mm]
- Load case
- Fx = 0
- Force
- Length of the beam
- Young's modulus
- Moment of inertia
The theoretical deflection is determined to w = 13.07 mm.
Simulation Iterations
- /BEAM
- /SHELL
- /BRICK
- /TETRA4
- /TETRA10
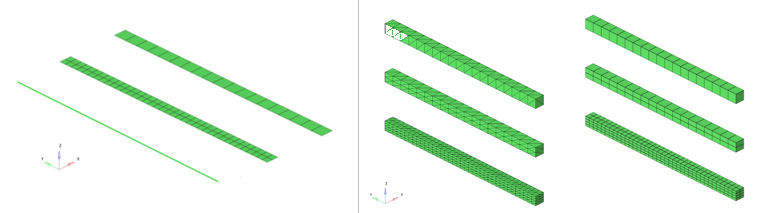
Figure 3. Different Meshes
- Cross section
- 100 mm2
- Moment of Inertia (bending)
- 833.33333 mm4
- Moment of Inertia (torsion)
- 1666.66666 mm4
For shell elements (/PROP/TYPE1 (SHELL)), several element formulations (Q4-shell with Ishell = 1, 2, 3, 4) are used. The results of modeling with QBAT-shell (Ishell = 12) and QEPH-shell (Ishell = 24) are compared.
For the solid mesh, the HA8 formulation (/PROP/TYPE14 (SOLID)) (Isolid = 14, 17, 18 and 24) are investigated. No reduced pressure integration is necessary for implicit computation, as the behavior is elastic (Icpre = 0).
For Tetra4 elements the formulations Itetra4 = 1, 1000 are used and for Tetra10 elements the formulations Itetra10 = 2, 100 are used.
Even though the displacement is small and a linear solver could be used, the nonlinear explicit and implicit solvers are used. The nonlinear implicit solver can be activated by using /IMPL/NONLIN.
The auto-defined adaptive damping (/ADYREL) is used to damp out the vibrations which are typical when a quasi-static problem is solved using an explicit solution.
Results
The displacement results in the table are reported at the main node of the rigid body attached to the end of the beam where the force is applied.
Explicit Solver
| Element | Mesh Size [mm] | Element Formulation | Maximum Deflection in Z-direction [mm] | Calculation Time [s] | Total Number of Cycles | Difference to Theoretical Value [%] |
|---|---|---|---|---|---|---|
| Beam | 10 | BEAMN3 | 13.035 | 78.53 | 767445 | 0.2 |
| 5 | 13.034 | |||||
| Q4 | 10 | Ishell = 3 | 13.032 | 80.87 | 607437 | 0.3 |
| 5 | 27.833 | 113 | ||||
| QBAT | 10 | Ishell = 12 | 12.839 | 154.01 | 621035 | 1.7 |
| 5 | 12.922 | 1.1 | ||||
| QEPH | 10 | Ishell = 24 | 12.975 | 94.97 | 601316 | 0.7 |
| 5 | 12.992 | 0.6 |
| Element | Mesh Size [mm] | Element Formulation | Maximum Deflection in Z-direction [mm] | Calculation Time [s] | Total Number of Cycles | Difference to Theoretical Value [%] |
|---|---|---|---|---|---|---|
| Tetra4 | 10 | Itetra4 = 1000 | 3.639 | 260.04 | 1034462 | 72 |
| 5 | 5.24 | 60 | ||||
| 2.5 | 9.168 | 30 | ||||
| Tetra4 | 10 | Itetra4 = 1 | 10.353 | 825.89 | 1034019 | 21 |
| 5 | 11.251 | 14 | ||||
| 2.5 | 12.472 | 5 | ||||
| Tetra10 | 10 | Itetra10 = 1000 | 13.381 | 3010.86 | 3207611 | 2 |
| 5 | 13.840 | 6 | ||||
| 2.5 | 13.626 | 4 | ||||
| Tetra10 | 10 | Itetra10 = 2 | 13.376 | 1605.92 | 1500391 | 2 |
| 5 | 13.842 | 6 | ||||
| 2.5 | 13.623 | 4 |
| Element | Mesh Size [mm] | Element Formulation | Maximum Deflection in Z-direction [mm] | Calculation Time [s] | Total Number of Cycles | Difference to Theoretical Value [%] |
|---|---|---|---|---|---|---|
| Hexa8 | 10 | Isolid = 14 | 12.965 | 434.18 | 845372 | 0.8 |
| 5 | 12.883 | 1.4 | ||||
| 2.5 | 12.934 | 1.0 | ||||
| Hexa8 | 10 | Isolid = 17 | 15.69 | 306.27 | 845442 | 20 |
| 5 | 9.915 | 24 | ||||
| 2.5 | 11.987 | 8 | ||||
| Hexa8 | 10 | Isolid = 18 | 12.965 | 417.45 | 845373 | 0.8 |
| 5 | 12.883 | 1.4 | ||||
| 2.5 | 12.934 | 1.0 | ||||
| Hexa8 | 10 | Isolid = 24 | 13.074 | 161.43 | 846398 | 0.1 |
| 5 | 12.941 | 0.9 | ||||
| 2.5 | 13.03 | 0.3 |
Implicit Solver
| Element | Mesh Size [mm] | Element Formulation | Maximum Deflection in Z-direction [mm] | Calculation Time [s] | Total Number of Cycles | Difference to Theoretical Value [%] |
|---|---|---|---|---|---|---|
| Beam | 10 | BEAMN3 | 13.03 | 13.68 | 32 | 0.3 |
| 5 | 13.03 | |||||
| Q4 | 10 | Ishell = 1 | 13.007 | 5.05 | 75 | 0.4 |
| 5 | 13.024 | 0.3 | ||||
| Q4 | 10 | Ishell = 2 | 13.011 | 17.07 | 33 | 0.4 |
| 5 | 13.037 | 0.2 | ||||
| Q4 | 10 | Ishell = 3 | 13.012 | 27.72 | 38 | 0.4 |
| 5 | 13.041 | 0.2 | ||||
| Q4 | 10 | Ishell = 4 | 13.011 | 17.64 | 33 | 0.4 |
| 5 | 13.037 | 0.2 | ||||
| QBAT | 10 | Ishell = 12 | 12.959 | 70.90 | 64 | 0.8 |
| 5 | 12.981 | 0.6 | ||||
| QEPH | 10 | Ishell = 24 | 12.964 | 13.95 | 32 | 0.8 |
| 5 | 12.979 | 0.7 |
| Element | Mesh Size [mm] | Element Formulation | Maximum Deflection in Z-direction [mm] | Calculation Time [s] | Total Number of Cycles | Difference to Theoretical Value [%] |
|---|---|---|---|---|---|---|
| Tetra4 | 10 | Itetra4 = 1000 | 3.64 | 13.69 | 32 | 71 |
| 5 | 5.24 | 59 | ||||
| 2.5 | 9.17 | 29 | ||||
| Tetra10 | 10 | Itetra10 = 1000 | 13.369 | 20.55 | 32 | 2 |
| 5 | 13.84 | 6 | ||||
| 2.5 | 13.616 | 4 |
| Element | Mesh Size [mm] | Element Formulation | Maximum Deflection in Z-direction [mm] | Calculation Time [s] | Total Number of Cycles | Difference to Theoretical Value [%] |
|---|---|---|---|---|---|---|
| Hexa8 | 10 | Isolid = 14 | 12.965 | 14.47 | 32 | 0.8 |
| 5 | 12.89 | 1.3 | ||||
| 2.5 | 12.939 | 1.0 | ||||
| Hexa8 | 10 | Isolid = 17 | 15.671 | 14.24 | 32 | 20 |
| 5 | 9.907 | 24 | ||||
| 2.5 | 11.98 | 8 | ||||
| Hexa8 | 10 | Isolid = 18 | 12.965 | 14.30 | 32 | 0.8 |
| 5 | 12.89 | 1.3 | ||||
| 2.5 | 12.939 | 1.0 | ||||
| Hexa8 | 10 | Isolid = 24 | 12.966 | 14.26 | 32 | 0.8 |
| 5 | 12.89 | 1.3 | ||||
| 2.5 | 12.939 | 1.0 |
Conclusion
- Explicit Solver
- Beam
- BEAM3N provides good results for the coarse and the fine mesh. The difference of deflection compared to the theoretical value is about 0.2%.
- Shells
- When the beam is modeled with shell elements, QEPH (Ishell = 24) will be the best element formulation. Compared to Q4-shells (Ishell = 3) and QBAT (Ishell = 12) it delivers the best results regarding mesh size, energy error, and very good precision versus cost. The QEPH formulation gives the same high quality results as the fully-integrated QBAT shell but at a much lower computational cost.
- Tetras
- Itetra4 = 1000 (default) elements are too stiff and do not give reasonable results, unless a fine mesh is used. Although a higher computational cost, the Itetra4 = 1 element formulation provides better results especially when a fine mesh is used.
- Bricks
- Hexa8 elements with Isolid = 24 element formulation provides the best results regarding mesh size, and calculation time. It also has very good precision versus cost ratio. The difference of deflection compared to the theoretical value is about 1%. Compared to the other element formulations calculation time is about 2 – 2.5 lower. When used with nonlinear materials, Isolid = 24 requires 3 or more elements through the thickness. For 1 or 2 elements through the thickness, a fully-integrated element like Isolid = 14 or 18 is recommended. The Isolid = 18 element automatically selects the best property settings depending on the material it is used with. The fully-integrated Isolid = 17 element suffers from shear locking which causes it to be too stiff and therefore not recommended.
- Implicit Solver
- Beam
- BEAM3N provides good results for the coarse and the fine mesh. The difference of deflection compared to the theoretical value is about 0.3%.
- Shells
- Shell elements with different element formulations provide good results regarding mesh size and calculation time. The difference of deflection to the theoretical value is under 1%. The QEPH shell shows best performance vs. precision ratio and is recommended.
- Tetras
- Tetra10 elements provide good results in terms of quality compared to tetra4 elements, which behave too stiff. The difference of deflection compared to the theoretical value varies between 2 to 6% and depends on the mesh size. For Tetra4 elements, the deflection compared to the theoretical value is to low, but converges with finer mesh size. The Itetra4 = 1 and Itetra10 = 2 elements are not supported in implicit analysis.
- Bricks
- Hexa8 elements with different element formulations provide good results for the coarse and the fine mesh, except for element formulation Isolid = 17 which suffers from shear locking. The difference of deflection compared to the theoretical value is about 1 %. The Hexa8 elements with Isolid = 24 show the best performance regarding precision of results and calculation time.