This subpanel creates three-dimensional partial torus surface primitives.
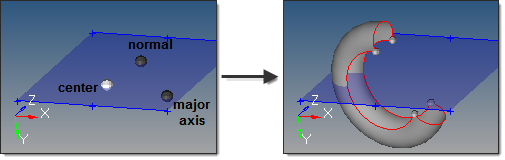
In this example, the major radius is 3 and major start/end angles are 30 and 270, while the minor
radius is 1 and the minor start/end angles are -120 and 120.
Nine inputs are required to create a torus using this method:
| • | The center node defines the absolute center of the torus. |
| • | The vector between the center node and the normal node is the torus axis. |
| • | The vector from the center node to the major axis node completes the definition of the torus plane. Combined with the normal node, this provides the complete torus orientation. |
| • | The major radius defines the outside radius of the torus, measured from the center node. |
| • | The major start angle defines the starting arc angle for the major circumference (ring), measured from the torus plane in a direction based on the torus axis using the right-hand rule. |
| • | The major end angle defines the ending arc angle for the major circumference (ring), measured from the torus plane in a direction based on the torus axis using the right-hand rule. The difference between this and the major start angle determines the major arc of the torus, and therefore the arc of the major cutout in the partial torus. For example, if your major start angle is 15 degrees, and your major end angle is 285 degrees, the resulting torus is an open ring with a 270 degree arc and a 90 degree cut. |
| • | The minor radius defines the radius of the circular cross-section of the torus. |
| • | The minor start angle defines the starting arc angle for the minor circumference (cross-section), measured from the mid-plane of the cross-section in a direction based on the cross-section centerline using the right-hand rule. |
| • | The minor end angle defines the ending arc angle for the minor circumference (cross-section), measured from the mid-plane of the cross-section in a direction based on the cross-section centerline using the right-hand rule. The difference between this and the minor start angle determines the minor arc of the torus, and therefore the arc of the minor cutout in the partial torus. For example, if your minor start angle is 15 degrees, and your minor end angle is 285 degrees, the resulting torus has a cross-section with a 270 degree arc and a 90 degree cut. |
How do I…
Create partial torus surface primitives
See also
Surfaces panel








