Fatigue Process Manager (FPM) using E-N (Strain - Life) Method

The E-N (Strain - Life) method should be chosen to predict the fatigue life when plastic strain occurs under the given cyclic loading. S-N (Stress - Life) method is not suitable for low-cycle fatigue where plastic strain plays a central role for fatigue behavior.

If an S-N analysis indicates a fatigue life less than 10,000 cycles, it is a sign that E-N method might be a better choice. E-N method, while computationally more expensive than S-N, should give reasonable estimate for high-cycle fatigue as well.

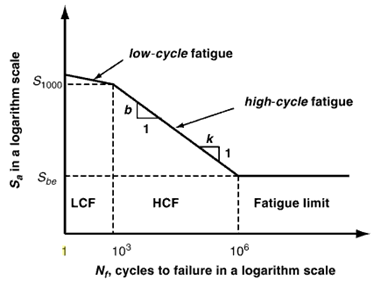
rd2070_SN_curve
Figure 1. Low Cycle and High Cycle regions on the S-N curve
Since E-N theory deals with uniaxial strain, the strain components need to be resolved into one combined value for each calculation point, at each time step, and then used as equivalent nominal strain applied on the E-N curve (Figure 2).

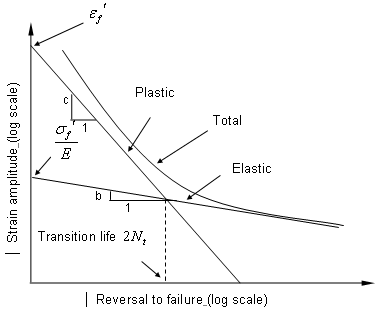
rd2080a_strainlife_curve
Figure 2. Strain-Life Curve

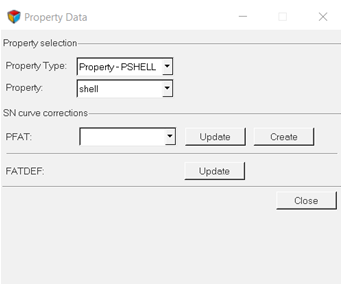
In OptiStruct, various strain combination types are available with the default being "Absolute maximum principle strain". In general "Absolute maximum principle stain" is recommended for brittle materials, while "Signed von Mises strain" is recommended for ductile material. The sign on the signed parameters is taken from the sign of the Maximum Absolute Principal value.

In this tutorial, you will be able to evaluate fatigue life with the E-N method.

The following files found in the optistruct.zip file are needed to perform this tutorial. Refer to Access the Model Files.

A control arm loaded by brake force and vertical force is used, as shown in Figure 3. Two load time histories acquired for 2545 seconds with 1 HZ, shown in Figure 4 and Figure 5, are applied. The material of the control arm is aluminum, whose E-N curve is shown in Figure 6. Because a crack always initiates from the surface, a skin meshed with shell elements is designed to cover the solid elements, which can improve the accuracy of calculation as well.

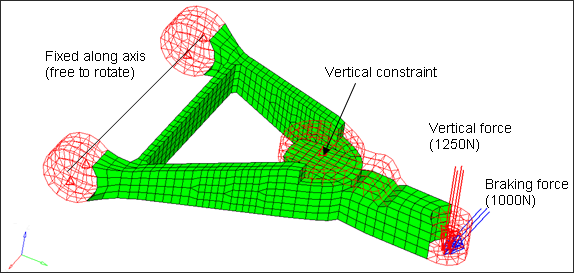
rd2070a_control_arm
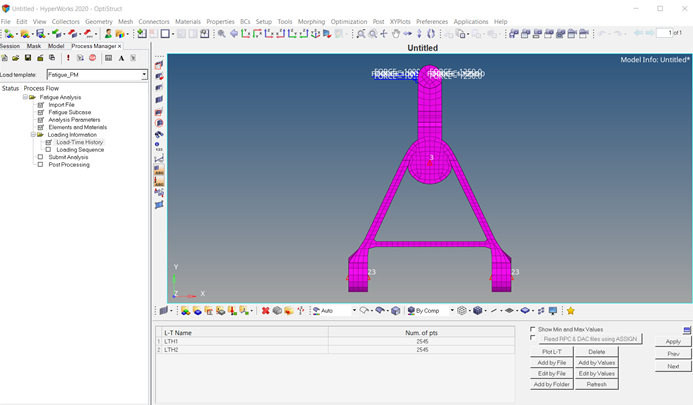
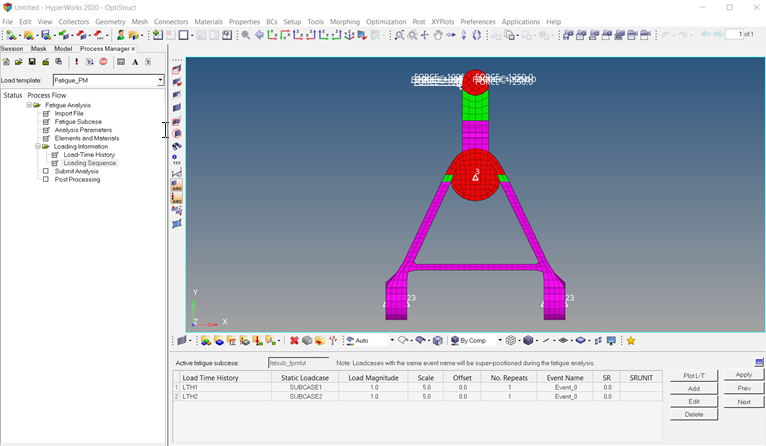
Figure 3. Model of Control Arm for Fatigue Analysis

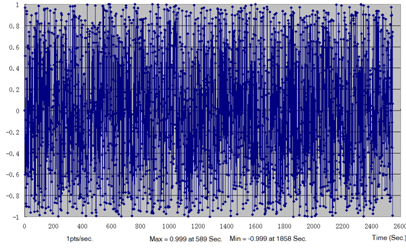
rd2070a_load_time
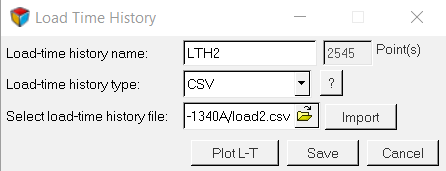
Figure 4. Load Time History for Vertical Force

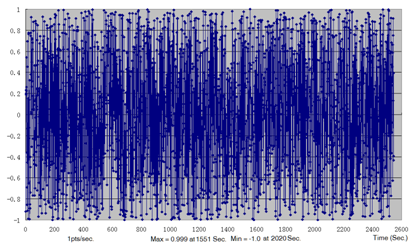
rd2070a_vertical_force
Figure 5. Load Time History for Braking Force

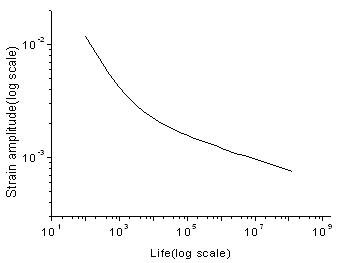
rd2080a_en_curve
Figure 6. E-N Curve of Aluminum

Launch HyperMesh and Process Manager

  1. Launch HyperMesh.
    The User Profile dialog opens.
  2. Select OptiStruct and click OK.
  3. Click Tools > Fatigue Process > Create New.
  4. For New Session Name, enter <my_session_name>.
  5. For Working Folder, select your working folder.
  6. Click Create.
    This creates a new file to save the instance of the currently loaded fatigue process template.


    Figure 7.

Import the Model

  1. Make sure the task Import File is selected in the Fatigue Analysis tree.
  2. For the Model file type, select OptiStruct.
  3. Click the Open model file icon files_panel.
    A Select File browser window opens.
  4. Select the ctrlarm.fem file you saved to your working directory from the optistruct.zip file and click Open.
  5. Click Import.
    This loads the control arm model. It includes a whole definition of two static subcases, elements sets, and material static properties, etc.
  6. Click Apply.
    This guides you to the next task Fatigue Subcase of the Fatigue Analysis tree.


    Figure 8. Import a Finite Element Model file

Set Up the Model

Create a Fatigue Subcase

  1. Make sure the task Fatigue Subcase is selected in the Fatigue Analysis tree.
  2. In the Create new fatigue subcase field, enter fatsub_fpmtut.
  3. Click Create.
  4. For the Select existing fatigue subcase field, select the newly created fatigue subcase fatsub_fpmtut.
    fatsub_fpmtut is selected as the active fatigue subcase. Definitions in the following processes (analysis parameters, fatigue elements and properties, loading sequences, etc.) will be for this subcase.
  5. Click Apply.
    This saves the current definitions and guides you to the next task Analysis Parameters of the Fatigue Analysis tree.


    Figure 9. Create and Select Active Fatigue Subcase to Process

Apply Fatigue Analysis Parameters

  1. Make sure the task Analysis Parameters is selected in the Fatigue Analysis tree.
  2. Select the following options:
    Analysis type
    E-N
    Stress combination method
    Signed von Mises
    FEA model unit
    MPA
    Mean stress correction
    SWT
    Rainflow type
    STRESS
    Plasticity correction
    NEUBER
  3. Enter the following values:
    Certainty of survivial
    0.5
    Gate
    0.0
  4. Click Apply.
    This saves the current definitions and guides you to the next task Elements and Materials of the Fatigue Analysis tree. For details, consult the Altair Simulation 2021.2 help.


    Figure 10. Fatigue Analysis Parameters Definition

Add Fatigue Elements and Materials

  1. Make sure the task Elements and Materials is selected in the Fatigue Analysis tree.
  2. Click Add Material.
    A Material Data window opens.
  3. For Material name, select Aluminum.
  4. Make sure Stress unit is set to MPA.
  5. For Ultimate tensile strength (UTS), enter 600.
  6. For Input method of Define EN Curve, select Estimate From UTS.


    Figure 11. Material Data Definition
  7. Click the Show EN curve definition icon 05_sn_curve.
    An EN method description window introducing how to generate the EN material parameter opens.
  8. Click Close.
  9. For Material type, select Aluminum and Titanium Alloys and click Estimate.
    All the data for EN curve definition are automatically estimated.
  10. Click Plot EN Curve at the bottom of the window to show the EN curve.
  11. Close the EN Curve plot window.
  12. Click Save to save the definition of the EN data for the selected entities.


    Figure 12.
  13. Click Add Property.
    A Property Data window opens.
  14. For Property Type, select Property - PSHELL.
  15. Click Create to create PFAT property.
  16. For LAYER, select TOP.
  17. For FINISH, select NONE.
  18. For TREATMENT, select NONE.
  19. Leave the field after KF (Fatigue strength reduction factor) set to 1.0.
  20. Click Close to save the definition of the EN data for the selected elements.
  21. Click Apply.
    This saves the current definitions and guides you to the next task Load-Time History of the Fatigue Analysis tree.

    rd2080b_mat_data
    Figure 13. Material Data Definition


    Figure 14. Elements and Material Definition

Add Load-Time History

  1. Make sure the task Load-Time History is selected in the Fatigue Analysis tree.
  2. Click Add by File.
    A Load Time History window opens.
  3. For Load-time history name, enter lth1.
  4. For Load-time history type, select CSV.
  5. Click the Open load-time file icon files_panel.
    An Open file browser window opens.
  6. Browse for load1.csv.
  7. Click Open > Import.
  8. Click Save to write the new load-time history into HyperMesh database.
  9. Create another load-time history named lth2 by importing the file load2.csv.

    rd2070b_load-time_dialog
    Figure 15. Import Load-Time History
  10. Click Plot L-T to show the load-time history.
  11. Close the Load Time History window.
  12. Click Apply.
    This saves the current definitions and guides you to the next task Loading Sequences of the Fatigue Analysis tree.

    rd2070b_load_time
    Figure 16. Load-time History Definition
    Note: For a file of DAC format, it can very easily be imported in HyperGraph and converted to CSV format for use by FPM.

Load Sequences

In this step, one event consisting of two load time history is created; in other words, the linear superposition of the stress caused by the two load time history is requested during analysis. Using this event, one load sequence is constructed.
  1. Make sure the task Loading Sequences is selected in the Fatigue Analysis tree.
  2. Click Add.
    A Load Mapping window opens.
  3. For Channels, select LTH1 and LTH2.
  4. For Subcase, select SUBCASE1 and SUBCASE2.
  5. Activate the radio button Auto and leave the event creation method set to default Single Event.
  6. Click + to create a single event with two subcases and two channels.


    Figure 17. Load Mapping to associate load-time history with static subcase
  7. Click Save to close the window and create the fatique event using selected subcases and channels.

    rd2080b_loading_sequence
    Figure 18. Loading Sequences Definition

Submit the Job

  1. Make sure the task Submit Analysis is selected in the Fatigue Analysis tree.
  2. Click the Save .fem file icon files_panel.
    A Save As browser window opens.
  3. Set the directory in which to save the file, and for File name, enter ctrlarm_fpmtut.fem.
  4. Click Save to close the window.
  5. Click Save to save the OptiStruct model file.
  6. For Run Option, select analysis.
  7. Click Submit.
    This launches OptiStruct 2021.2 to run the fatigue analysis. If the job is successful, the new results files should be in the directory from which was selected.
    The default files written to the directory are:
    ctrlarm_fpmtut.0.3.fat An ASCII format file which contains fatigue results of each fatigue subcase in iteration step.
    ctrlarm_fpmtut.h3d Hyper 3D binary results file, with both static analysis results and fatigue analysis results.
    ctrlarm_fpmtut.out OptiStruct output file containing specific information on the file set up, the set up of your fatigue problem, compute time information, etc. Review this file for warnings and errors.
    ctrlarm_fpmtut.stat Summary of analysis process, providing CPU information for each step during analysis process.
    Note: The filename.#.fat is created for each fatigue subcase at the first and last iterations only if a fatigue optimization is performed.


    Figure 19. Submit Fatigue Analysis

Post-process the Analysis

  1. Make sure the task Post-processing is selected in the Fatigue Analysis tree.
    When fatigue analysis has completed successfully after the previous submit, it will automatically go into this task.
  2. For Fatigue subcase, make sure Select Subcase is selected.
  3. For Result Type and Data Component, select the required data you want to contour from the drop-down menu.
  4. Click Load H3D Results (HV).
    This launches HyperView and loads the ctrlarm_fpmtut.h3d results file. It applies the result contour for selected result type and component. You can use HyperView for more detailed results.
  5. Click Exit to unload Fatigue Process Manager.


    Figure 20. Post-Processing


    Figure 21. Damage Contour in HyperView