Lid-Driven Cavity in 2D
Problem Description
A square cavity with a side length of L°= 1e-3° m is filled with water (density: 1000 kg/m3, dynamic viscosity: 1e-3 kg/m/s). The upper wall is moved with a constant velocity U0 imposing a rotational movement of the fluid in the cavity. Here, the configurations with Re°=°100, Re°=°1000 and Re°=°10000 are simulated by adjusting the velocity of the lid correspondingly. The highly-resolved Finite-Difference calculations by Ghia et al. #reference_fql_tlv_s2b__fn_fbf_tmv_s2b with a grid resolution of 257x257 are taken as reference.
Numerical Setup

Figure 1. Initial Particle Distribution of the 50x50 Case
Results
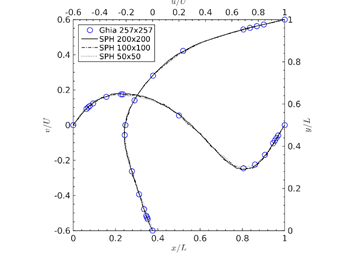
Figure 2. Profiles of the Re=100 Case
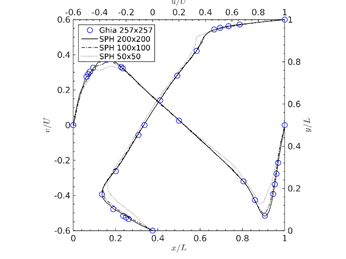
Figure 3. Profiles of the Re=1000 Case
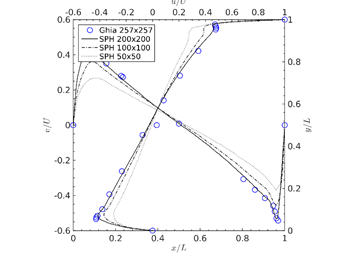
Figure 4. Profiles of the Re=10000 Case
S. Adami, H. Hu and N. Adams, "A generalized wall boundary condition for smoothed particle hydrodynamics," Journal of Computational Physics, vol. 231, pp. 7057-7075, 2012.
U. Ghia and K. S. C. Ghia, "High-Re solutions for incompressible flow using the Naview-Stokes equations and a multigrid method," Journal of Computational Physics, vol. 48, pp. 387-411, 1982.