Backward-Facing Step in 2D
Problem Description
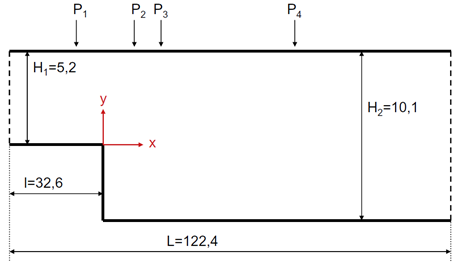
Figure 1. Sketch of the Backward-Facing Step from Adami et al (lengths in mm). See #reference_qvv_r3v_s2b__fn_ij4_4kv_s2b
Numerical Setup
Two particle resolutions are simulated, with a cutoff length rc°=°0.2*S for the coarser and rc°=°0.1*S for the finer resolution. For the initial particle configuration, the particles are distributed on a Cartesian grid. The walls boundary conditions are imposed according to the methodology described by Adami et al. #reference_qvv_r3v_s2b__fn_zdx_xkv_s2b
Results

Figure 2. Visualization of the Flow Behind the Step for the Fine Resolution at Steady-State
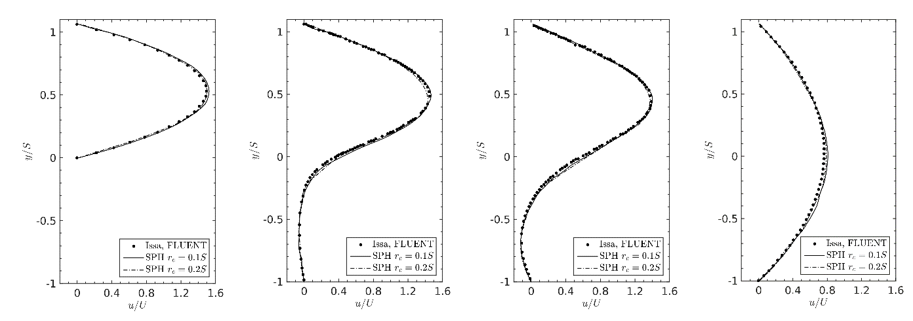
Figure 3. Velocity Profiles at the Reference Positions P1 to P4 (from left to right)
S. Adami, H. Hu and N. Adams, "A generalized wall boundary condition for smoothed particle hydrodynamics," Journal of Computational Physics, vol. 231, pp. 7057-7075, 2012.
R. Issa, Numerical assessment of smoothed particle hydrodynamics gridless method for incompressible flows and its extension to turbulent flows, PhD Thesis: University of Manchester, 2005.
S. Adami, X. Hu and N. Adams, "A transport-velocity formulation for smoothed particle hydrodynamics," Journal of Computational Physics, vol. 241, pp. 292-307, 2013.