Flow Inside a Rotating Cavity
In this application, AcuSolve is used to simulate the flow of air in an enclosed cylindrical cavity with a rotating top and a fixed bottom. AcuSolve results are compared with experimental data adapted from Michelsen (1986). The close agreement of AcuSolve results with experimental data validates the ability of AcuSolve to model cases containing enclosed cavities with flow induced by rotating walls.
Problem Description
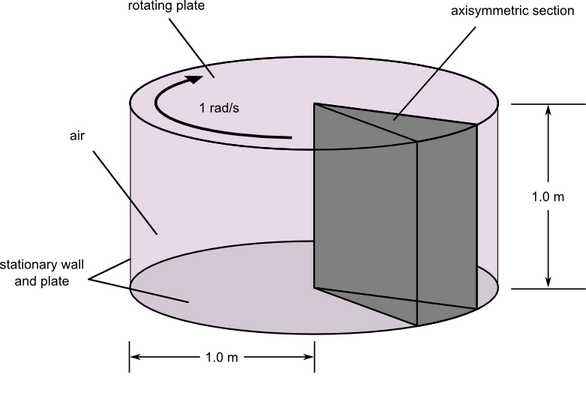
Figure 1. Critical Dimensions and Parameters for Simulating Flow Inside a Rotating Cavity
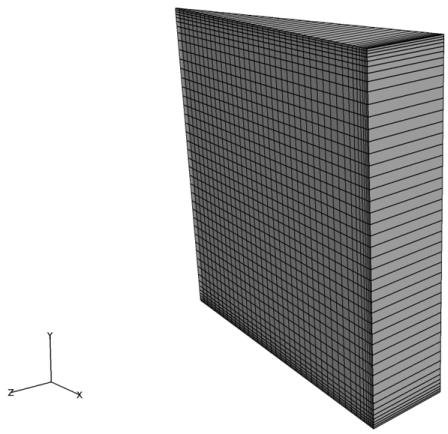
Figure 2. Mesh of Periodic Section Used for Simulating Flow Inside a Rotating Cylinder
AcuSolve Results
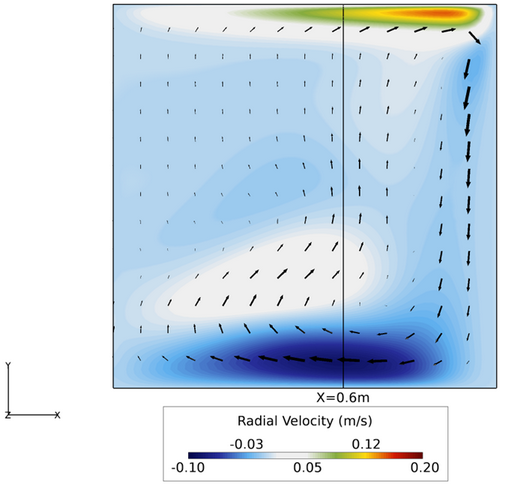
Figure 3. Contours of Radial Velocity with Velocity Vectors. This Image Shows the Front Face of the Modeled Cylinder Wedge, with the Center of Rotation on the Left Edge. The Vertical Line Represents a Radial Location 0.6 m From the Center of Rotation.
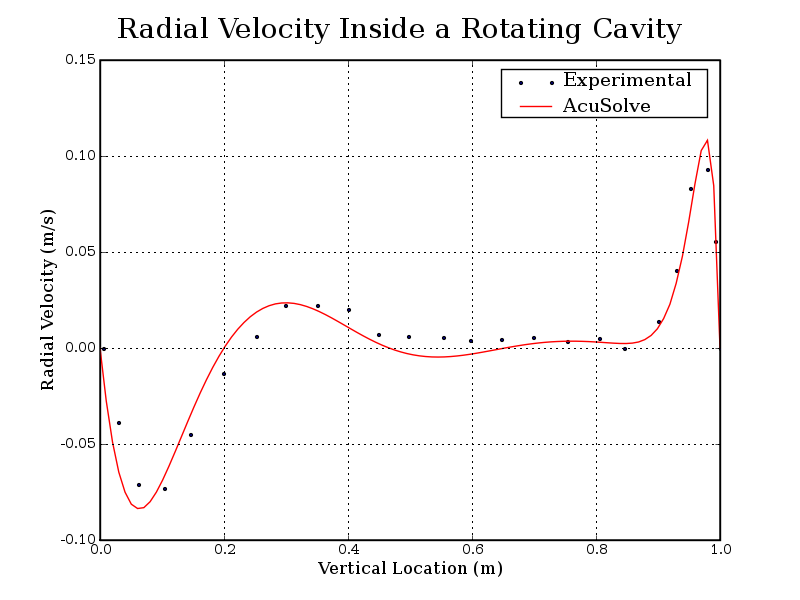
Figure 4. Radial Velocity (at 0.6 m From the Center of Rotation) as a Function of Vertical Location From Cylinder Bottom
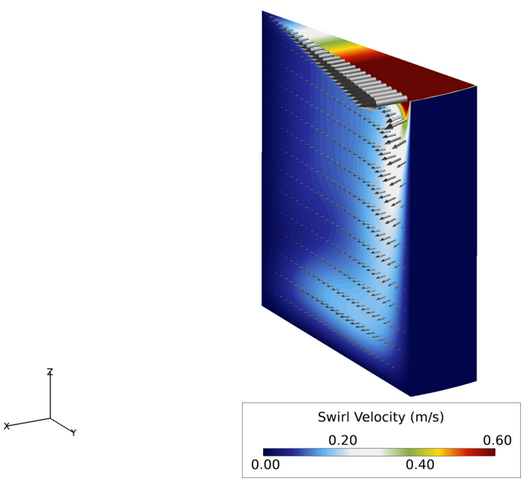
Figure 5. Contours of Swirl Velocity with Velocity Vectors
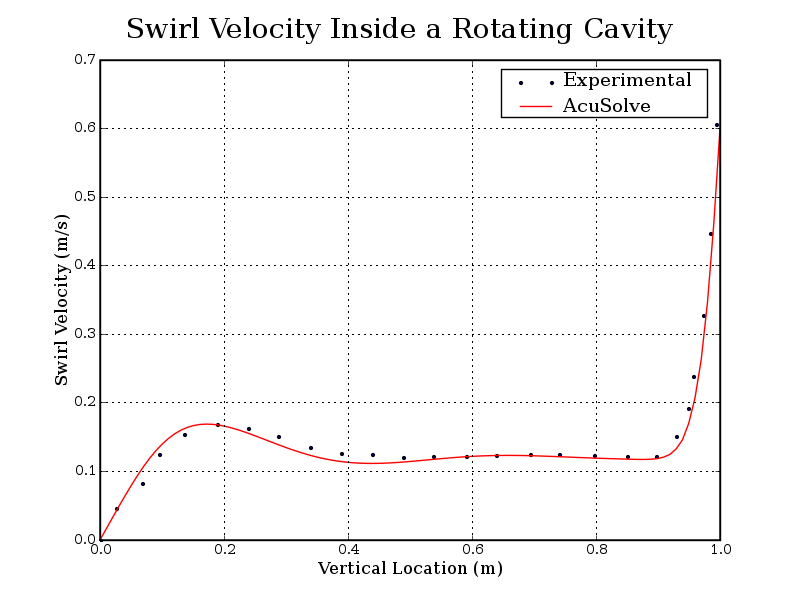
Figure 6. Swirl Velocity (at 0.6 m From Center of Rotation) as a Function of Vertical Location From the Cylinder Bottom
Summary
The AcuSolve solution compares well with the experimental data for flow induced by a rotating top of an enclosed cylinder. In this application, the flow in the fluid region is driven by the viscous stresses near the rotating top. Viscous stresses drag the fluid in a circular direction near the spinning wall. The angular velocity of the fluid decreases as distance from the top wall increases. Radial velocity develops as a result of the migration of the fluid toward the outer wall in regions of high angular velocity. The AcuSolve radial and swirl velocities compare very closely with the experimental data.
Simulation Settings for Flow Inside a Rotating Cavity
AcuConsole database file: <your working directory>\cavity_rotating\cavity_rotating.acs
Global
- Problem Description
- Analysis type - Steady State
- Turbulence Equation - Laminar
- Auto Solution Strategy
- Relaxation Factor - 0.4
- Material Model
- Air
- Density - 1.0 kg/m3
- Viscosity - 0.000556 kg/m-sec
- Air
- Reference Frame
- Cavity Rotation
- Rotation center
- X-coordinate - 0.0
- Y-coordinate - 0.0
- Z-coordinate - 0.0
- Angular velocity
- X-component - 0.0
- Y-component - -1.0 rad/sec
- Z-component - 0.0
- Rotation center
Model
- Cavity Rotation
- Volumes
- Fluid
- Element Set
- Material model - Air
- Element Set
- Fluid
- Surfaces
- Bottom
- Simple Boundary Condition
- Type - Wall
- Simple Boundary Condition
- Max_X
- Simple Boundary Condition
- Type - Wall
- Simple Boundary Condition
- Max_Z
- Simple Boundary Condition - (disabled to allow for periodic conditions to be set)
- Min_Z
- Simple Boundary Condition - (disabled to allow for periodic conditions to be set)
- Top
- Simple Boundary Condition
- Type - Wall
- Reference frame - Cavity Rotation
- Simple Boundary Condition
- Bottom
- Periodics
- Periodic 1
- Periodic Boundary Condition
- Type - Axisymmetric
- Rotation axis
- point 1
- X-coordinate - 0.0 m
- Y-coordinate - 0.0 m
- Z-coordinate - 0.0 m
- point 2
- X-coordinate - 0.0 m
- Y-coordinate - 1.0 m
- Z-coordinate - 0.0 m
- point 1
- Periodic Boundary Condition
- Periodic 1
References
J. A. Michelsen. "Modeling of Laminar Incompressible Rotating Fluid Flow". AFM 86-05. Ph.D. thesis, Department of Fluid Mechanics, Technical University of Denmark. 1986.