Simplex (Nelder-Mead)
The Simplex Nelder-Mead Algorithm can be categorised as a local or hill-climbing search method, where the final optimum relies strongly on the specified starting point.
The geometric figure formed by a set of N+1 points in an N-dimensional space is called a simplex. The basic idea in the simplex method is to compare the values of the combined goals at the N +1 points of a general simplex (where each point represents a single set of parameter values) and move the simplex gradually toward the optimum point during an iterative process. The movement of the simplex is achieved using three operations: reflection, contraction and expansion.
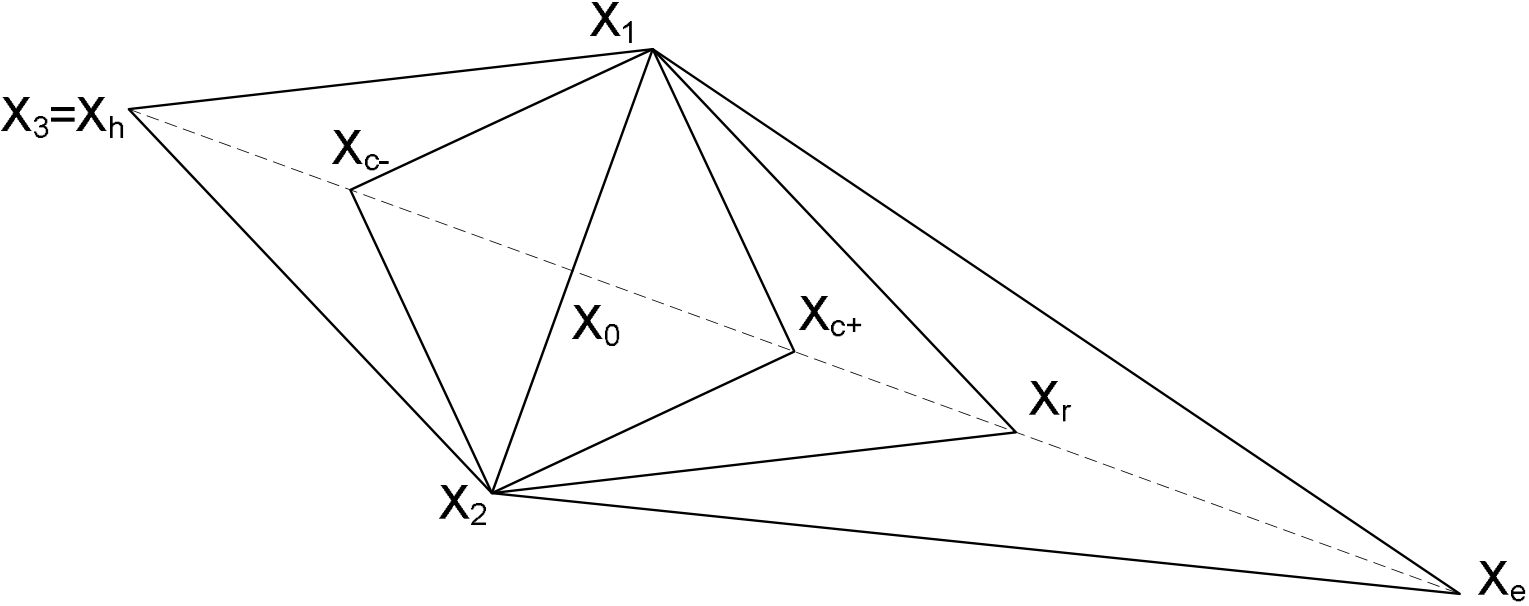
Figure 1. Reflection, expansion and contraction for the Simplex method.
Reflection
Consider the diagram in Figure 1. If Xh is the point corresponding to the poorest fitness value among the points of the initial simplex, it may be expected that the point Xr obtained by reflecting the point Xh around the axis defined by the other points in the simplex (X1 and X2) may (when evaluated according to the optimisation goals) provide a better fitness value. If this is the case, a new simplex can be constructed by rejecting the point Xh from the simplex and including the new point Xr. This process is illustrated in Figure 1 where the points X1, X2 and Xr form the new simplex. Since the direction of movement of the simplex is always away from the worst result, movement will always be in a favourable direction. If the global goal function does not have steep valleys within the space defined by the parameter ranges, repetitive application of the reflection process will lead to a zigzag path in the general direction of the optimum.
Expansion
If a reflection process finds a point Xr which is a better fitness than any point in the simplex (a new optimum point), it may be expected that the best fitness value may be improved even further by moving along the direction pointing from X0 to Xr. An expansion is therefore performed from Xr to Xe.
If the evaluated fitness at Xe is better than the fitness at Xr, the expansion was successful; Xh his then replaced with Xe and the reflection process is restarted. If the evaluated fitness at Xe is poorer, the expansion attempt has failed; Xh is replaced by Xr (as identified in the previous reflection operation) and the reflection process is continued.
Contraction
If the reflection process finds a point Xr with a better fitness than the second-best point in the current simplex (Xnh), a contraction operation will be performed.
If the contraction process produces a point Xc which has a better fitness than a point in the simplex, the contraction was successful and Xh is replaced with Xc before continuing with the reflection process. If the contraction process produces a point Xc which has a poorer fitness, the contraction process has failed and the simplex base is reduced by scaling all the points in the simplex by an internal factor before restarting with the reflection process.
| Objective Function | Operation |
|---|---|
| F(Xr) < F(Xl) | Expansion |
| F(Xl) ≤ F(Xr) < F(Xnh) | Reflection |
| F(Xnh) ≤ F(Xr) < F(Xh) | Positive contraction |
| F(Xh) ≤ F(Xr) | Negative contraction |
Error treatment and termination
- The maximum number of Feko solver runs has been reached
- The standard deviation between the simplex vertices is small enough
- The simplex base is small enough
- The optimisation goal has been reached
Text log
During an optimisation, OPTFEKO maintains a text log of the optimisation process in the project .log file. The structure of this file is primarily determined by the optimisation method.
========================= L O G - FILE - OPTFEKO =========================
Version: 13.22 of 2007-05-08
Date: 2007-06-06 16:45:43
File: test
OPTIMISATION WITH ALtair Feko
=============== Optimisation variables ===============
No. Name Beg.value Minimum Maximum
1 sigma 3.503500000e+07 1.000000000e+07 5.000000000e+08
=============== Optimisation goals ===============
No. Name Expression
1 search1.goals.nearfieldgoal1 nearfieldgoal1 =============== Optimisation method: SIMPLEX NELDER-MEAD ===============
Maximum number of iterations: 1000
Base of the simplex: 1.500000000e-01
Reduction factor of the base: 5.000000000e-01
Termination at minimal base: 1.000000000e-03
Termination at standard deviation: 1.000000000e-04
Standard reflection coefficient (R): 1.000000000e+00
Contraction coefficient (-C, +C): 5.000000000e-01
Expansion coefficient (E): 2.000000000e+00
=============== SIMPLEX NELDER-MEAD: Intermediate results ===============
No. sigma nearfieldgoal1 global goal operation global best aim
1 3.503500000e+07 6.488107157e-02 3.488107157e-02 ----- 3.488107157e-02
2 3.774988237e+07 5.929294284e-02 2.929294284e-02 ----- 2.929294284e-02
3 4.516707895e+07 6.328463622e-02 3.328463622e-02 -----
4 4.788196133e+07 5.795280540e-02 2.795280540e-02 R 2.795280540e-02
5 5.430544199e+07 5.500882669e-02 2.500882669e-02 E success 2.500882669e-02
6 4.153550651e+08 3.036429062e-02 3.642906239e-04 R 3.642906239e-04
7 4.356175335e+08 2.964433899e-02 3.556610122e-04 E success 3.556610122e-04
8 4.457496125e+08 2.929870383e-02 7.012961666e-04 R
9 4.356179559e+08 2.964446921e-02 3.555307926e-04 +C success 3.555307926e-04=============== SIMPLEX NELDER-MEAD: Finished ===============
Optimisation finished (Standard deviation small enough: 5.020322005e-06)
Optimum found for these parameters:
sigma = 4.356179559e+08
Optimum aim function value (at no. 9): 3.555307926e-04
No. of the last analysis: 9
Sensitivity of optimum value with respect to each optimisation parameter,
i.e. the gradient of the aim function at 1% variation from the optimum:
Parameter Sensitivity
sigma 8.344260771e-01