Tutorial: Co-Simulation with MotionSolve
Learn how to build a Multi-Body System Model (MBS) of an inverted pendulum, combine it with a controls system model, and co-simulate the models.
Files for This Tutorial
Inverted_Pendulum_Tutorial.scm; Inverted_Pendulum_Tutorial.mdl
Overview of Co-Simulation and Prerequisites
Co-simulation enables MotionSolve Multi-Body Dynamics (MBS) models and Activate models to communicate with each other during simulation.
An ideal use case for co-simulation is the development of a control system for an MBS model. This tutorial shows you how to develop such a control system for an inverted pendulum.
An inverted pendulum is a pendulum that has its center of mass above its pivot point, such as a pendulum moving horizontally with its pivot point mounted on a moving railroad cart. Whereas a normal pendulum is stable when hanging downward, an inverted pendulum is inherently unstable, and must be actively balanced in order to remain upright either by applying a torque at the pivot point or by moving the pivot point horizontally as part of a feedback system.
This tutorial shows you how to design a control force acting horizontally on a cart to keep a pendulum upright, much like a child balancing a stick on his hand. The inverted pendulum is a classic problem in dynamics and control theory and is used as a benchmark for testing control strategies. Some real-world examples of inverted pendulum problems include attitude control of a rocket at launch, and the balance and movement of a Segway motorized vehicle.
Prerequisites
The installation of HyperWorks MotionSolve software is required for co-simulation. MotionSolve offers powerful modeling, analysis, visualization and optimization capabilities for multi-disciplinary simulations that include kinematics and dynamics, statics and quasi-statics, linear and vibration studies, stress and durability, loads extraction, co-simulation, effort estimation, and packaging synthesis.
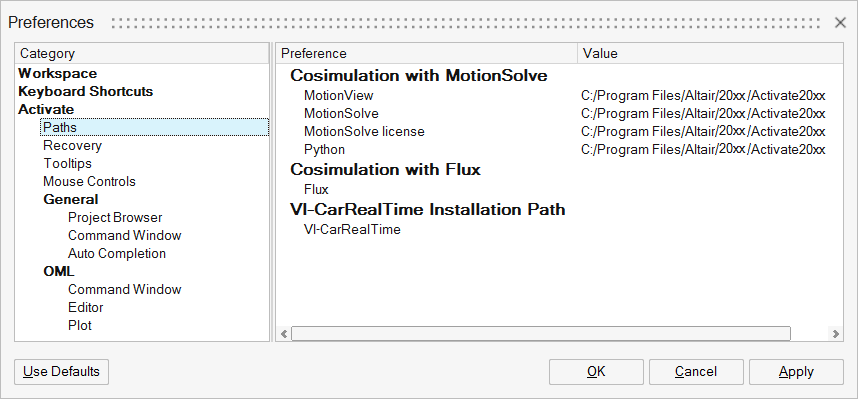
Defining the Software Path Settings
Defining the paths to MotionSolve and other software that is required for local and remote co-simulation methods.
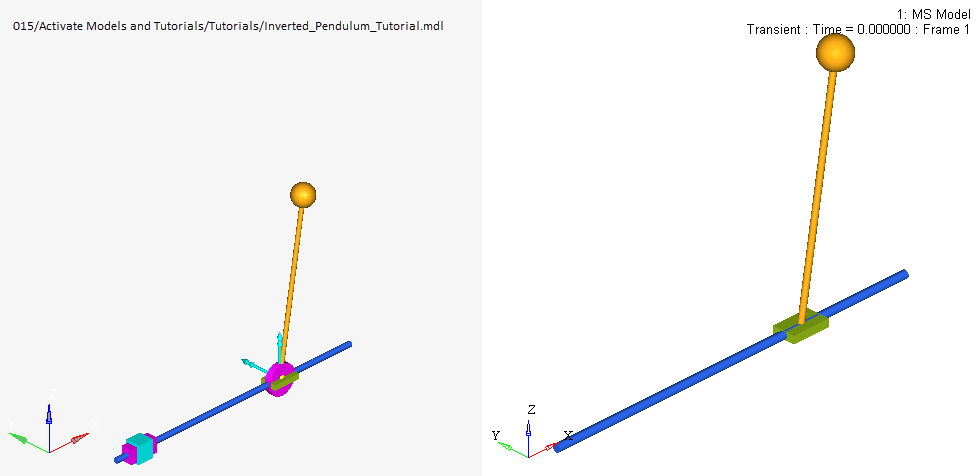
Building an Inverted Pendulum
Build a Multi-Body System (MBD) model of an inverted pendulum on a cart.
Entities in the MBS Model
- Pendulum
- Cart
- Rod to connect the pendulum to the cart
- Rail on which the cart is constrained to move horizontally
- Pivot which is located on the cart, between the pendulum and cart
Building the Geometry
With MotionView software, create the geometry for the inverted pendulum.
Adding Bodies
Add the pendulum and cart to your model.
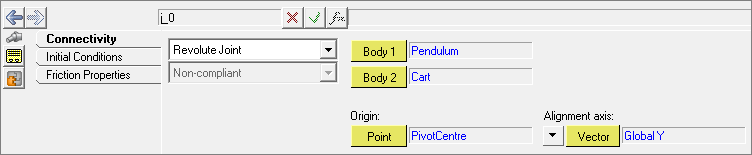
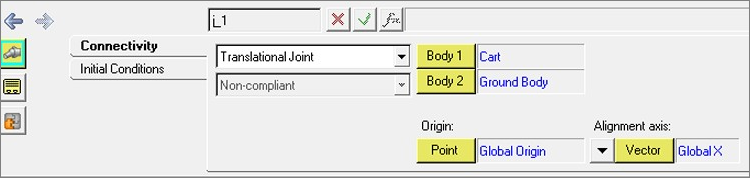
Adding Joints
Add a revolute and translational joint to the model.
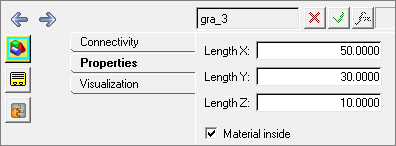
Adding Graphics
Graphics are essential for understanding the model behavior in an animation.
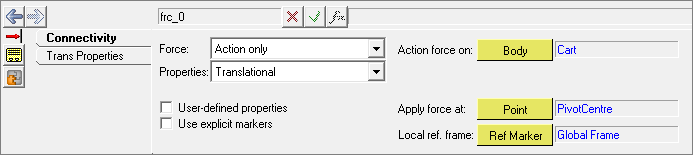
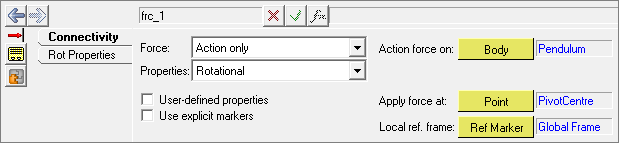
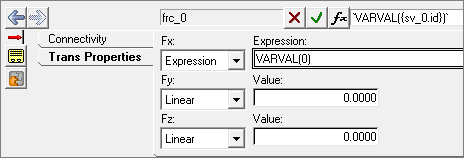
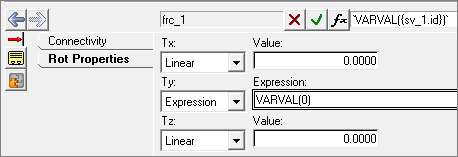
Adding Forces
Apply translational forces to the Cart.
Modifying the MBS Model for Co-Simulation
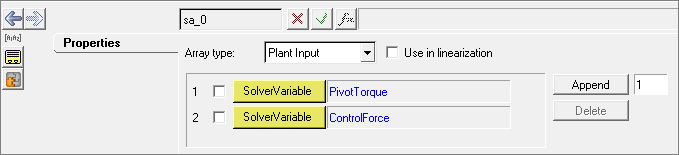
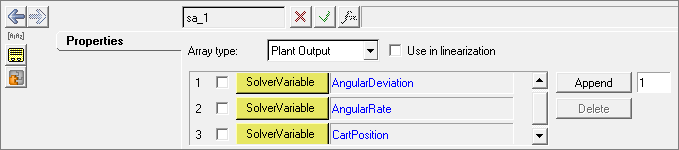
Modify the basic MBS model for co-simulation by adding MotionView entities including solver arrays and solver variables.
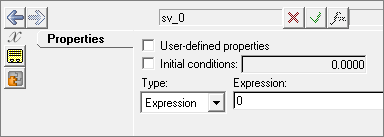
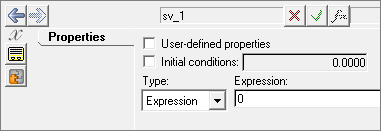
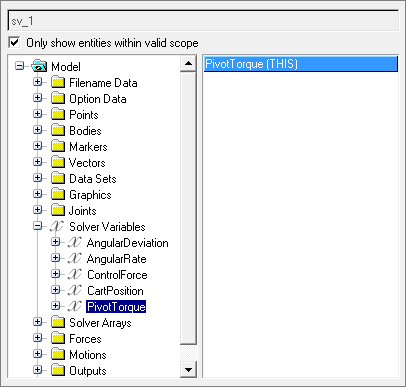
Adding Solver Variables
Validating the Inverted Pendulum Model
Simulate the MBS model in MotionSolve and validate that it performs as required.
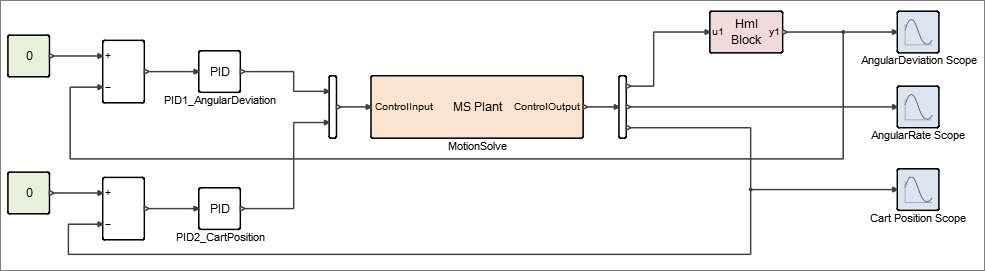
Building the Controls System Model
Build a controls system model with Activate.
The controls system model requires these blocks:
| Block | Description |
|---|---|
| MotionSolve | Enables the embedding of a MotionSolve model into an Activate model. |
| Mux | Reads multiple signals into one signal. |
| Demux | Reads a signal which contains multiple components and splits the signal into individual components. |
| OMLCustomBlock | |
| Scope | Plots data as defined. |
| Constant | Generates a command signal. |
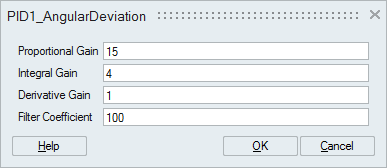
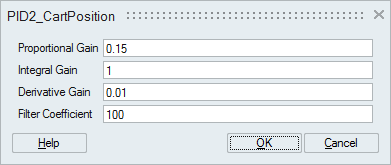
| PID | Serves as the controller block, the brain of the model. |
| Sum | Calculates the error from reference signals and feedback. |