This option gives an adiabatic pressure volume relation. With
= 1 an isothermal condition can also be applied. It is possible to
define an incompressible sub-volume to model a volume partially filled with a liquid.
The
general equation is:
(1)
With
-
- Initial volume
-
- Incompressible volume
A viscosity
can be used to reduce numerical oscillations.
If
= 1 a critical damping (shell mass and volume stiffness) is used. The
viscous pressure
is:
(2)
Where,
-
- Mass of fabric
-
- Its surface
The applied pressure is
.
The specific inputs for this type are:
-
-
-
-
-
If the deflation is considered (isenthalpic outflow computation), the initial mass
of gas, must also be input.
This monitored volume is typically used to model tire pressure
or simple fuel tank. For tire model
is zero and for fuel tank
is the fuel volume.
Thermodynamical Equations
The basic energy equation of the monitored volume can be written as:
(3)
Where,
-
- Internal energy
-
- Pressure
-
- Monitored volume
-
- Incompressible volume
-
- Outgoing enthalpy
When the adiabatic condition is applied and assuming a perfect gas:
(4)
Where,
is the gas constant. For air,
= 1.4.
The two equations above allow the current volume to be determined. The energy and pressure can then be found.
External Work Variation
At the current time step,
, assume we know:
-
-
-
will be obtained as:
(5)
be the variation of external work and from the adiabatic condition:
(6)
we have:
(7)
Let:
(8)
Hence, the external work is given by:
(9)
Computing the energy from basic principles:
(10)
can be estimated from,
, the velocity at vent hole; this estimation will be
described hereafter.
The variation of internal energy
can be given by:
(11)
Therefore:
(12)
(13)
This pressure is then applied to the monitored volume to get:
- New accelerations
- New velocities
- New geometry
- New volume
- Ready for next step evaluation
Venting
Venting, or the expulsion of gas from the volume, is assumed to be isenthalpic.
The flow is also assumed to be unshocked, coming from a large reservoir and through a small
orifice with effective surface area,
.
Conservation of enthalpy leads to velocity,
, at the
vent hole. The Bernouilli equation is then written as:
(14)
(monitored volume) 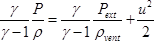 (vent hole)
(vent hole)
Applying the adiabatic conditions:
(15)
Therefore, the exit velocity is given by:
(16)
The mass flow rate is given by:
(17)
The energy flow rate is given by:
(18)
The vent hole area or scale factor area,
, can be defined in these ways:
- a constant area taking into account a discharge coefficient
- a variable area equal to the area of a specified surface, multiplied by a discharge
coefficient
- a variable area equal to the area of the deleted elements within a specified surface,
multiplied by a discharge coefficient
Supersonic Outlet Flow
Vent pressure
is equal to external pressure
for unshocked flow. For shocked flow,
is equal to critical pressure
and
is bounded to critical sound speed:
(19)
And,
(20)
,
)
Example: GAS Type
Some applications in
Radioss:
- A tire model:
The inputs are:
-
= 1.4
-
-
= 105 Pa
-
= initial tire pressure
Then, the pressure in the tire is
-
- A fuel tank model if the sloshing effect is neglected
Only if the sloshing effect is
neglected, pressure in a partial filled fuel tank can be modeled with a type GAS monitored
volume. Use the following input:
-
= 1.4
-
-
= 105 Pa
-
= 105 Pa
-
= volume of fuel
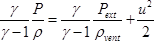 (vent hole)
(vent hole)