Lagrangian and Corotational Formulations
- Total Lagrangian description (TL)
- The FEM equations are formulated with respect to a fixed reference configuration which is not changed throughout the analysis. The initial configuration is often used; but in special cases the reference could be an artificial base configuration.
- Updated Lagrangian description (UL)
- The reference is the last known (accepted) solution. It is kept fixed over a step and updated at the end of each step.
- Corotational description (CR)
- The FEM equations of each element are referred to two systems. A fixed or base configuration is used as in TL to compute the rigid body motion of the element. Then the deformed current state is referred to the corotated configuration obtained by the rigid body motion of the initial reference.
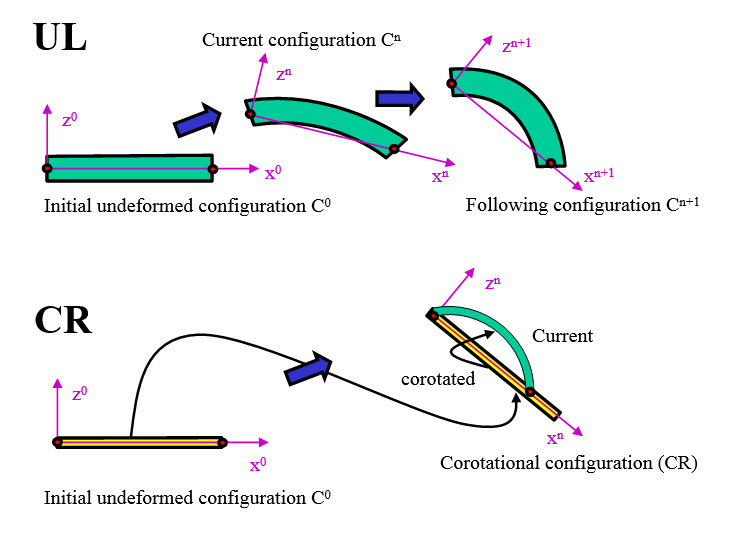
Figure 1. Updated Lagrangian and Corotational Descriptions
By default, Radioss uses a large strain, large displacement formulation with explicit time integration. The large displacement formulation is obtained by computing the derivative of the shape functions at each cycle. The large strain formulation is derived from the incremental strain computation. Hence, stress and strains are true stresses and true strains.
The derivatives are with respect to the spatial (Eulerian) coordinates. The weak form involves integrals over the deformed or current configuration. In the total Lagrangian formulation, the weak form involves integrals over the initial (reference) configuration and derivatives are taken with respect to the material coordinates.
The corotational kinematic description is the most recent of the formulations in geometrically nonlinear structural analysis. It decouples small strain material nonlinearities from geometric nonlinearities and handles naturally the question of frame indifference of anisotropic behavior due to fabrication or material nonlinearities. Several important works outline the various versions of CR formulation. 1 2 3 4 5