MV-2051: Frequency Response Analysis using MotionSolve and Compose
In this tutorial, you will learn how to convert a multibody model to its equivalent state space form using MotionSolve and obtain corresponding matrices, use these state space matrices to construct an equivalent LTI system of the multibody model within Altair’s Compose, and perform a frequency response analysis on the LTI system by plotting a Bode Plot diagram.
This is an extension of tutorial - MV-2050: Linear Analysis for Stability and Vibration Analysis.
Control system design becomes computationally simpler using mathematical tools like transfer function that can only be applied on Linear time-invariant systems (LTI systems). Linear systems have outputs as a linear combination of inputs. A wide range of physical systems can be approximated very accurately by LTI models.
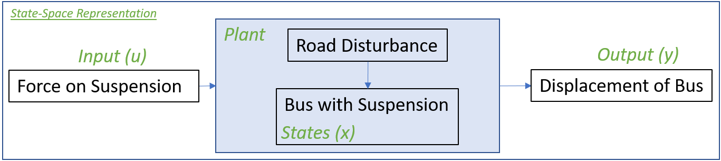
A Linear Time Invariant (LTI) system in the state space form is described as follows:
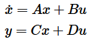
where A, B, C, and D are the state matrices, x is the state vector, u is the input vector, and y is the output vector.
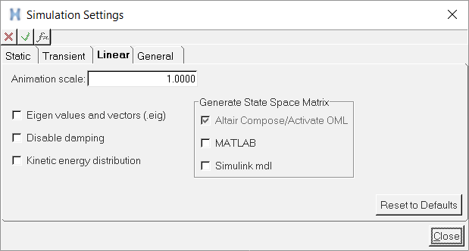
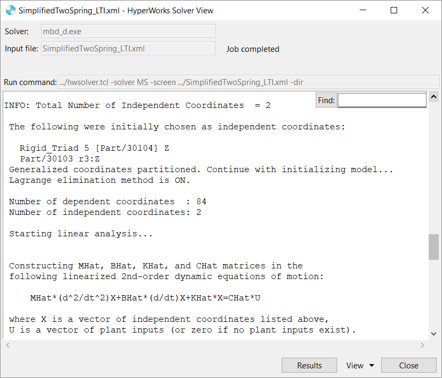
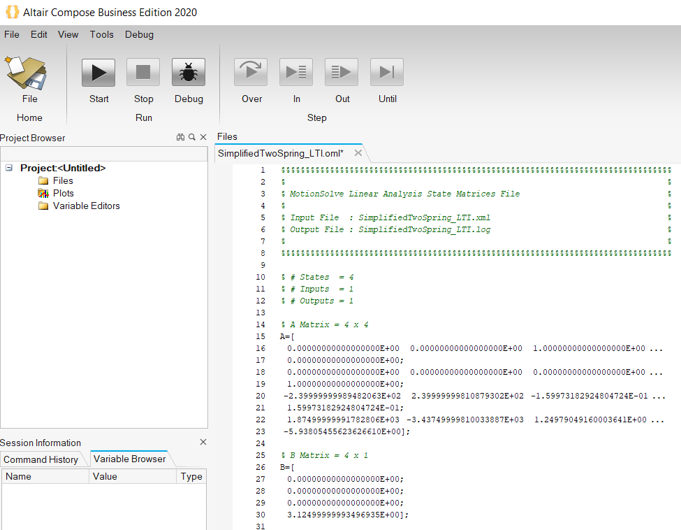
MotionSolve can linearize a multibody system by calculating the state matrices for a given set of inputs and outputs through a linear analysis. The states are chosen automatically by MotionSolve.
Frequency response concepts and techniques play an important role in control system design and analysis. In frequency-response methods, we vary the frequency of the input signal over a certain range and study the resulting response.
In this tutorial, you will learn how to convert a multibody model to its equivalent state space form using MotionSolve and obtain corresponding A, B, C and D matrices. These state space matrices will be further used to construct an equivalent LTI system of the multibody model within Altair’s Compose. Next, a frequency response analysis will be performed on the LTI system using Compose by plotting a Bode Plot diagram.
Next, you can then perform control system design using a variety of tools available within Compose, however this is out of the scope of this tutorial.
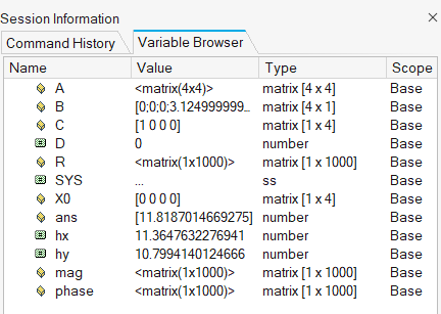
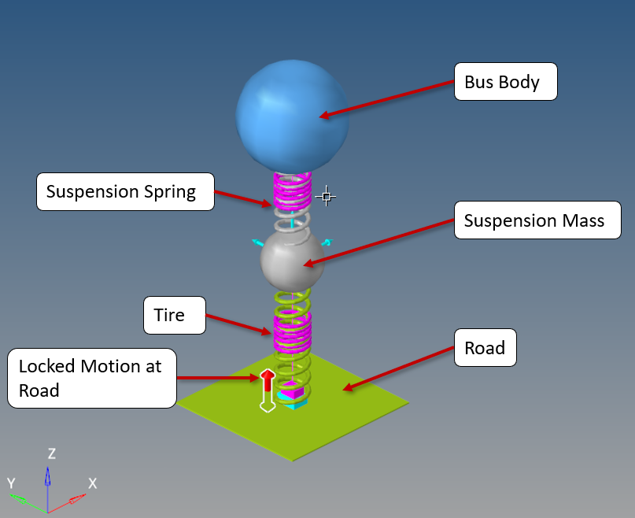
Open and Review the Model
Transient Analysis - Response at First Mode
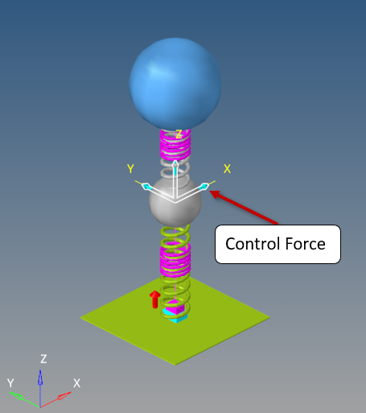
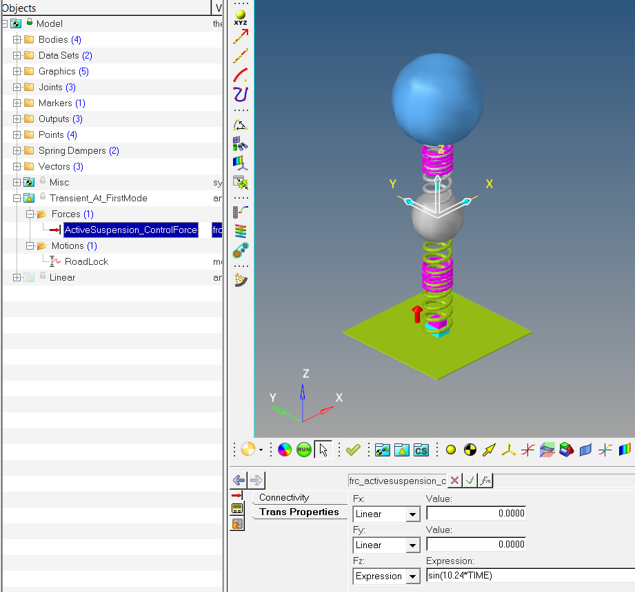
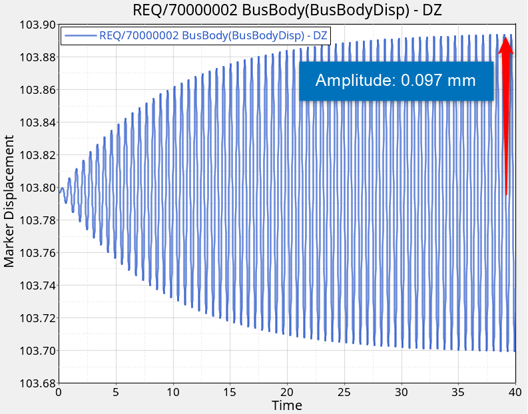
In previous tutorial (MV-2050) the first mode of this system was identified at 1.63Hz (~10.24 rad/s). In this step you will identify the response of this system (in other words, Displacement of Bus) when a unit force is applied at a forcing frequency of 10.24rad/s at Suspension Body.
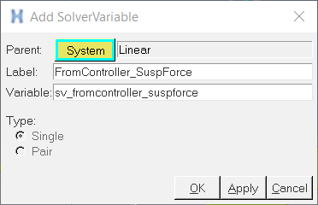
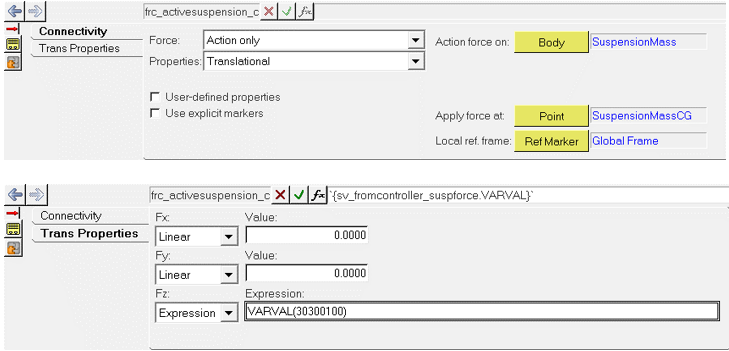
Linear Analysis - Plant Input
In this step you will setup the input of the plant (u). A control force will be applied on the Suspension Mass.
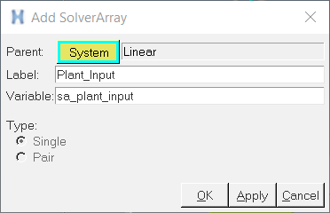
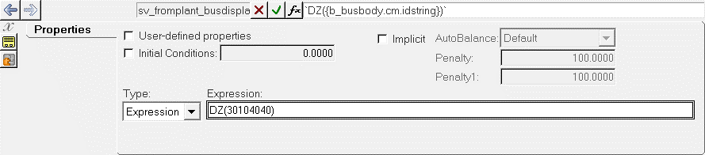
Linear Analysis - Plant Output
In this step you will set up the output of the plant (y). A solver variable and solver array will be added to the Linear analysis in a similar way shown in Step #3 above.
Set Up and Run a Linear Analysis
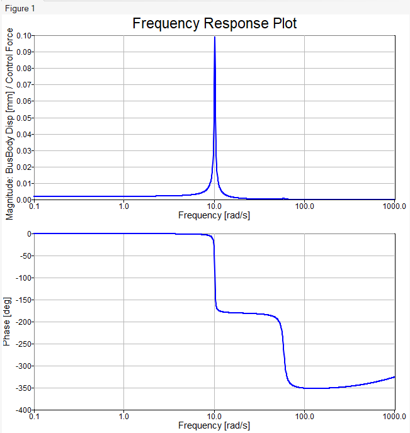
Frequency Response Analysis in Compose
In this step you will perform a frequency response analysis in Compose using the state space model from MotionSolve. Note that the during the run, an input signal of varying frequencies is supplied to the LTI system and due to its property, the magnitude and phase of the output signal changes while the frequencies itself remain the same.




 the oml script
the oml script

 button.
button.