Basis Functions
Basis functions are elementary functions for the modelling of the unknown quantity on a mesh element.
Categories of Basis Functions
- entire-domain basis functions
- sub-domain (sub-sectional) basis functions
Entire-domain basis functions are defined over the entire surface of the scatterer - they are non-zero over the entire domain. The formulation of these functions is deemed rather trivial, provided the shape of the scatterer is regular. For most practical applications, the shape of the scatterer is irregular and the formulation of such basis functions is near impossible. This requires the usage of sub-domain basis functions.
Types of Sub-Domain Basis Functions
- constant (also known as pulse or stair-step)
- linear
- polynomial
- piecewise sinusoidal
The Rao-Wilton-Glisson (RWG) element
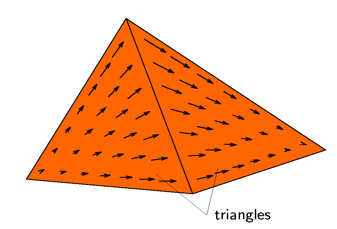
Figure 1. A triangle pair showing the current flow across the common edge as modelled by the RWG basis function.
In Figure 1, only two triangles are shown sharing a common edge. Each triangle also has two other edges. If these edges are connected to triangles, then additional basis functions would be required. Therefore for a triangle connected on all three sides, a total of three basis functions would be defined. Within the triangle element the total current would then be the sum of these three basis functions.
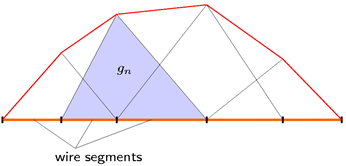
Figure 2. Linear roof-top basis functions for wires modelling current across the wire vertices.