MV-9003: LuGre Friction Tutorial
In this tutorial, you will learn how to implement and use a new MotionSolve object.
- Create a friction force on a translational joint using the LuGre friction model, and using Object Oriented Design with classes.
A class is a blueprint, or template, that allows you to create a higher level entity and treat it just like any other MotionSolve object.
In this example, you will combine a series of MotionSolve entities into a class called LuGre to define a new modeling element that exhibits new behavior. This process is called aggregation and MotionSolve provides a special composite class to represent such objects.
Composite is a special class that allows you to aggregate entities, such as parts, markers, forces, differential equations, and other MotionSolve primitives. A composite class object behaves just like any other solver object except it is a collection of entities conveniently packaged together. They behave as atomic entities and can be instantiated multiple times.
The advantage of using the composite class is that the LuGre object inherits behaviors from the base class. In particular, you will be able to modify the LuGre object at run-time, just like you would issue a modify command on any other MotionSolve primitive object, such as a part or a marker. The example below illustrates how you can create your own composite class. First, you'll examine the LuGre friction model.
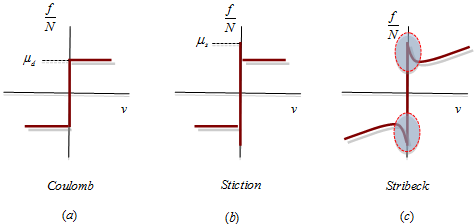
LuGre Friction Model
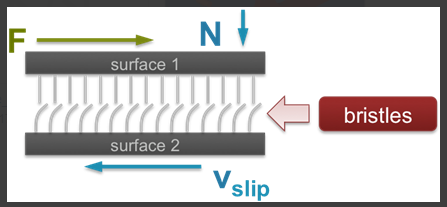
Figure 1.
- = Stiction to dynamic friction transition velocity
- = Coefficient of static friction
- = Coefficient of dynamic friction
- = Bristle stiffness
- = Bristle damping
- = Viscous coefficient
- Velocity in joint v =
- Stribeck factor
- The normal force
- Coulomb friction
- Static Friction
- ODE defining bristle deflection
- The friction force
- DIFF defining the bristle deflection
- MARKER defining the point of action of the friction force
- FORCE defining the friction element
- REQUEST capturing the friction force on the block
Load the Msolve Module
Create a Model
Now that you have completely defined the LuGre class and implemented the two methods (Sforce and Diff), you have to create a suitable model for testing.
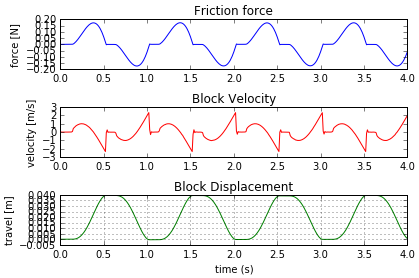
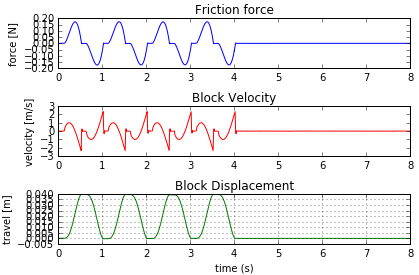
You can use a simple friction element defined between two bodies on a sliding block. The sliding block is constrained by a translational joint and a forcing function acts upon it.
You can study the effect of changing the Static Friction Coefficient μs on the computed friction force by modifying it between simulations.
The model is created inside a function, called _slidingblock, in the code cell below. This is done purely for convenience.