MV-3000: DOE using MotionView - HyperStudy
- Use HyperStudy to set-up a DOE study of a MotionView model
- Perform DOE study in the MotionView – HyperStudy environment
- Create approximation (using the DOE results) which can be subsequently used to perform optimization of the MotionView model
Theory
HyperStudy allows you to perform Design of Experiments (DOE), optimization, and stochastic studies in a CAE environment. The objective of a DOE, or Design of Experiments, study is to understand how changes to the parameters (design variables) of a model influence its performance (response).
After a DOE study is complete, approximation can be created from the results of the DOE study. The approximation is in the form of a polynomial equation of an output as a function of all input variables. This is called as the regression equation.
The regression equation can then be used to perform Optimization.
HyperStudy can be used to study different aspects of a design under various conditions, including non-linear behavior.
- Provides a variety of DOE study types, including user-defined
- Facilitates multi-disciplinary DOE, optimization, and stochastic studies
- Provides a variety of sampling techniques and distributions for stochastic studies
- Parameterizes any solver input model via a user-friendly interface
- Uses an extensive expression builder to perform mathematical operations
- Uses a robust optimization engine
- Includes built-in support for post-processing study results
- Includes multiple results formats such as MVW, TXT for study results
Tools
- From the Menu bar, select Applications >HyperStudy
You can then select MDL property data as design variables in a DOE or an optimization exercise. Solver scripts registered in the MotionView Preferences file are available through the HyperStudy interface to conduct sequential solver runs for DOE or optimization.
For any study, the HyperStudy process is shown below:
Figure 1.
The HyperStudy Process
MotionView MDL files can be directly loaded into HyperStudy. Any solver input file, such as MotionSolve, ADAMS, or Abaqus, can be parameterized and the template file submitted as input for HyperStudy. The parameterized file identifies the design variables to be changed during DOE, optimization, or stochastic studies. The solver runs are carried out accordingly and the results are then post-processed within HyperStudy.
Copy the files hs.mdl and target_toe.csv, located in the mbd_modeling\doe folder, to your <working directory>.
In the following steps, you will create a study to carry out subsequent DOE study on a front SLA suspension model.
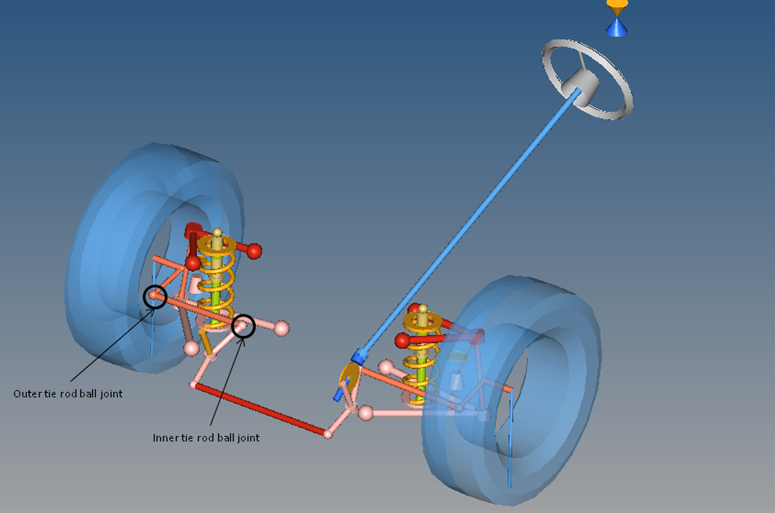
Figure 2.
While performing a Static Ride Analysis, you will determine the effects of varying the coordinate positions of the origin points of the inner and outer tie-rod joints on the toe-curve.
Step 1: Study Setup
- Start a new MotionView session.
-
Click the Open Model icon,
 ,
on the Model-Main toolbar.
,
on the Model-Main toolbar.
Or, from the menu bar, select File > Open > Model.
- Select the file model hs.mdl, located in your <working directory>, and click Open.
- Review the model and the toe-curve output request under Static Ride Analysis.
-
From the Applications menu, select HyperStudy.
HyperStudy is launched. The message "
Establishing connection between MotionView and HyperStudy
" is displayed. -
Start new study using one of the following ways:
- From the Welcome page, click the New Study icon,
 .
. - From the toolbar, click the New Study icon,
 .
. - From main menu, select File > New. The HyperStudy - Add Study dialog is displayed.
Figure 3. - From the Welcome page, click the New Study icon,
-
Accept the default label name.
- Under Location, click the file browser and select <working directory>\.
- Click OK.
-
Model definition.
- From the study Setup tree, select Define models.
-
Click
 to open the Add Model dialog.
to open the Add Model dialog.
- Under Type, select MotionView to add a MotionView model to the study.
- Accept the default variable name.
-
Click OK.
The following table with model data is created.

Figure 4.
-
Model data.
Please note that following details are automatically filled when you define the model (previous step).
- Under Active, check the box to activate or deactivate the model from study.
- The label of model entered in previous step.
- The variable name of model entered in the previous step.
- The model type selected in previous step.
- Point to the source file (here model file is sourced from MotionView through the MotionView – HyperStudy interfacing).
- Enter a name for the solver input file with the proper extension (for MotionSolve .xml) and select the solver execution script MotionSolve - standalone ( ms).
-
Create design variables.
- Click Import Variables to specify the design variables for the study.
- The Model Browser window opens in MotionView, allowing you to select the variables interactively.
-
Select the following from the browser using the
Model Parameter Tree dialog:
System Point Coordinate Function Front SLA susp. Otr tie-rod ball-jt -left Y Double-click or Click Add Front SLA susp. Otr tie-rod ball-jt –left Z Double-click or Click Add Parallel Steering Inr tie-rod ball - left Y Double-click or Click Add Parallel Steering Inr tie-rod ball - left Z Double-click or Click Add 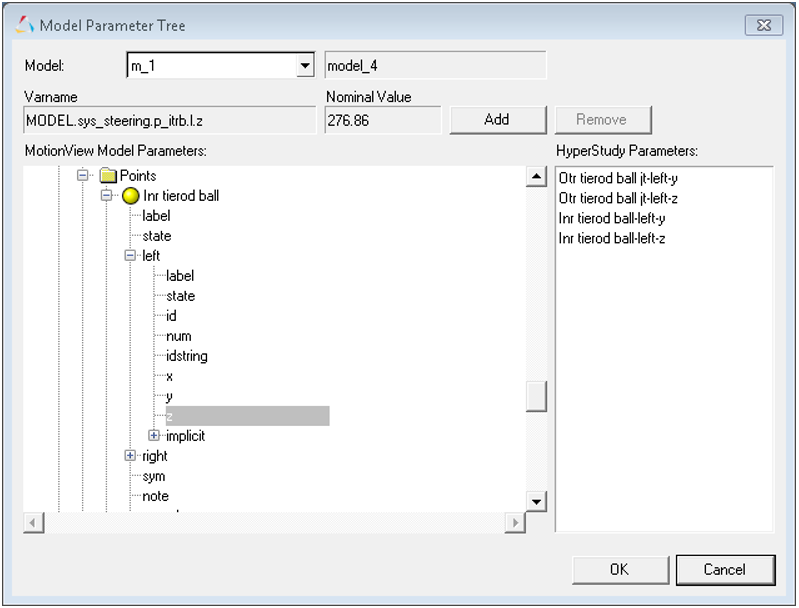
Figure 5. Model Parameter Tree dialog - Click Done.
- Click Next to go to Define Design Variables.
-
Define design variables.
-
From the Define design variables tab, edit the upper and lower bounds
of the design variables according to the following table.
Point Coordinate Lower Upper Outer tie-rod ball-jt -left Y -571.15 -559.15 Outer tie-rod ball-jt - left Z 246.92 250.92 Inner tie-rod ball - left Y -221.9 -209.9 Inner tie-rod ball - left Z 274.86 278.86 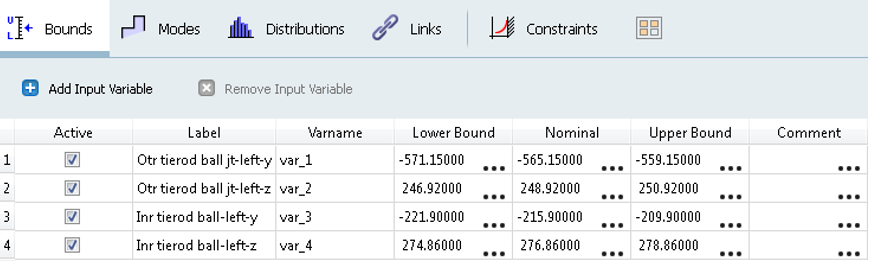
Figure 6. - This step also includes definition of other properties to the design variables. The options Details and Distributions specify variations of design variables in the range specified. The option Link Variables is used to link different design variables through a mathematical expression.
- Click on each tab to observe these options.
-
Right click on the column header row to view more options that you may
want to add.
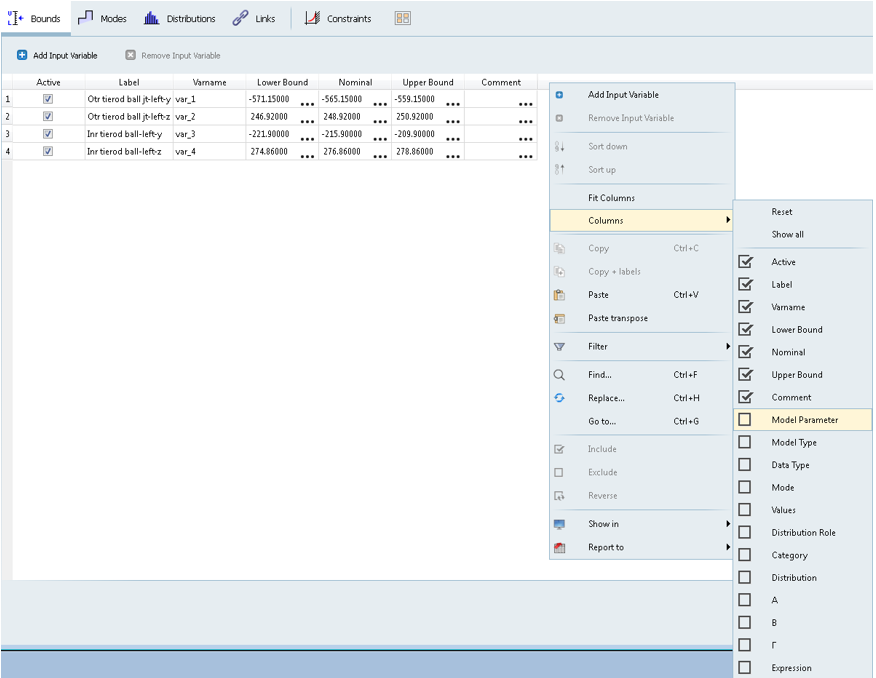
Figure 7. - Click Next to go to Specifications.
-
From the Define design variables tab, edit the upper and lower bounds
of the design variables according to the following table.
-
Test models.
This section allows you to perform a test run to verify that HyperStudy is able to execute a run and extract the results from the same by accessing its files.
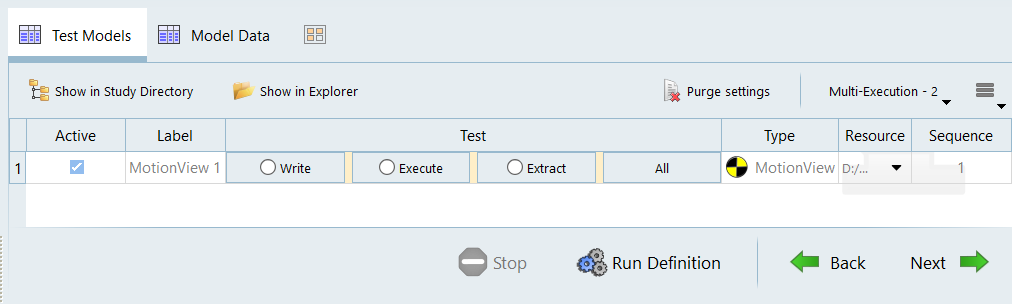
Figure 8.-
Click Run Definition to start the process.
Note: Once finished, green checkmarks will be present next to the following options: Write, Execute, and Extract.
- Click Next to go to Define Output Response.
-
Click Run Definition to start the process.
-
Define Response.
- Click Add Response to add a new response.
- Label the response Sum of Squared Error.
-
Accept the variable name and click OK.

Figure 9. Response table data -
Click the ellipses, …, in the Expression cell of Response table to
launch the Expression Builder.
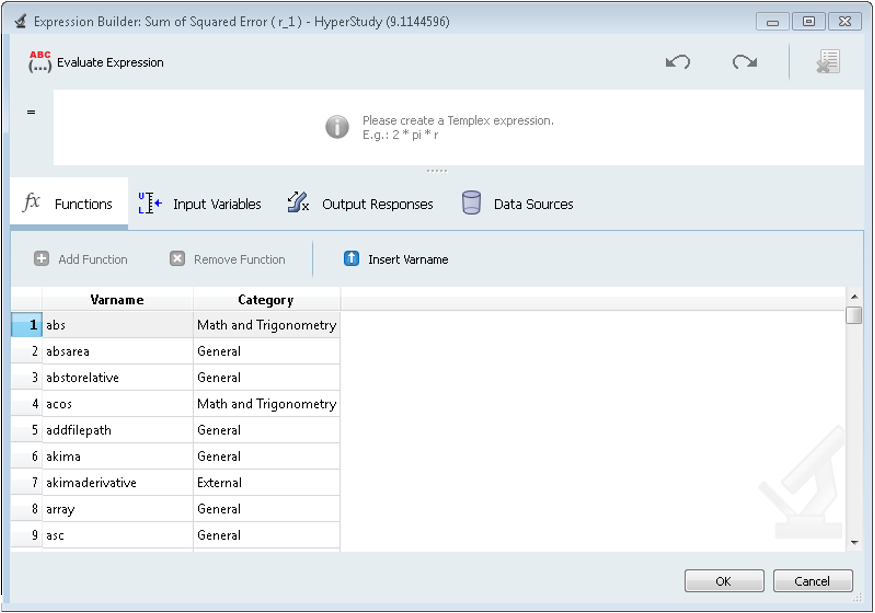
Figure 10. Expression BuilderNote: You can move the cursor over the function to display the function help. For this exercise, the response function requires two Data Sources:- The elements of Data Source 1 contain actual data points of the toe curve from the solver run for the nominal configuration.
- The elements of Data Source 2 contain data points from the target curve.
- Click the Data Sources tab to source the data from the files.
-
Data Source 1
-
Click to add a new data source using the solver output file.

Figure 11. Response data table - Click the ellipses, …, in the File cell of Data Source table data to launch the Data Source Builder: Data Source 1 (ds_1) dialog box.
-
Click the file browser button,
 , and select the file
m_1.mrf from <working
directory>\approaches\setup_1-def\run__00001\m_1\.
, and select the file
m_1.mrf from <working
directory>\approaches\setup_1-def\run__00001\m_1\.
- This enables the Type, Request and Component fields.
- From the Type drop-down menu, select Expressions.
- From the Request drop-down menu, select REQ/70000033 toe-curve.
-
From the Component drop-down menu, select
F2.
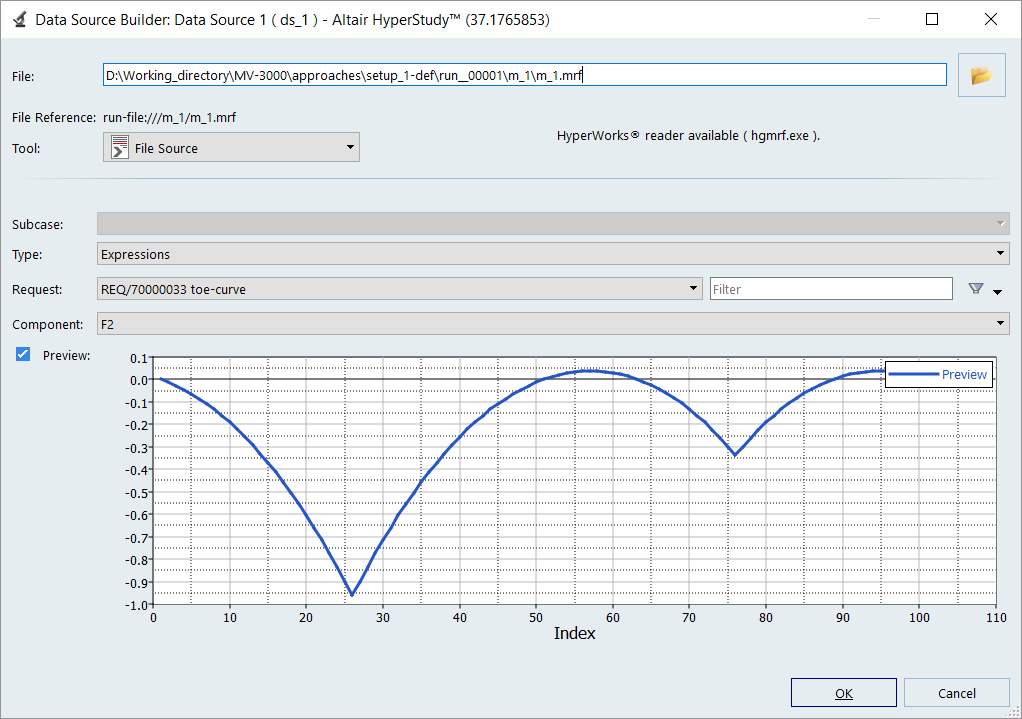
Figure 12. Data Source 1 dialog boxYou have now selected the toe curve data from the solver run as the data elements for Data Source 1.
- Click OK.
-
Click to add a new data source using the solver output file.
-
Data Source 2
- Create a Data Source to hold the data elements from the target toe curve.
-
Click Add Data Source to add a new data source
using a reference file.

Figure 13. Response data table - Click the … in the File cell of the Data Source 2 table data to launch the Data Source Builder: Data Source 2 (ds_2) dialog box.
-
Click the file browser button,
 , and select the file target_toe.csv, located in
your <working directory>\.
, and select the file target_toe.csv, located in
your <working directory>\.
- Set Type to Unknown and Request to Block 1.
- From the Component drop-down menu, select Column 1.
- Click OK.
-
In the Expression field, create the following expression:
sum((ds_1-ds_2)^2)
This expression evaluates the sum of the square of the difference between the “actual toe change” values (from solver run) and the “targeted toe curve” (from imported file). In the next tutorial, MV-3010, we will use HyperStudy to minimize the value of this expression to get the required suspension configuration.
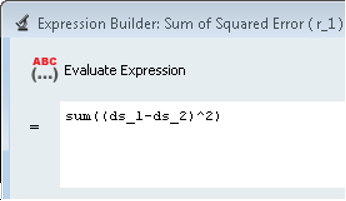
Figure 14. - Click Evaluate expression to verify that the expression is evaluated correctly. You should get a value of 16.284.
- Click OK to close the Expression builder and hit the Evaluate button.
- From the File menu, select Save As….
- Save this study set-up as setup.hstudy to your <working directory>\.
Step 2: DOE Study
-
Adding new DOE study.
-
Right-click in the Explorer browser area and from the context menu,
click Add to display the Add Approach
dialog.
Figure 15. -
Use Next button to add a new DOE study.
Figure 16.Note: Observe an Add Approach dialog is displayed.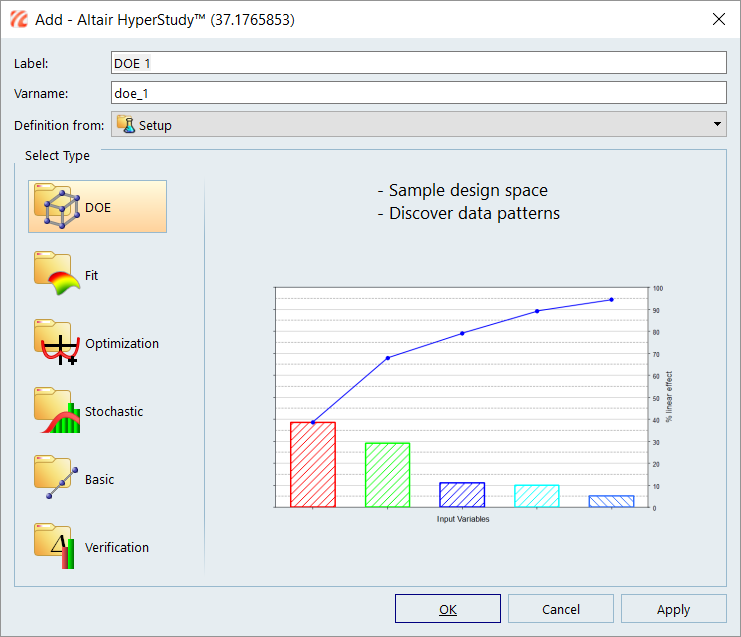
Figure 17. - Under Select Type, select Doe.
-
Accept the default label and variable name and click
OK.
The DOE study tree is displayed in the Browser with name Doe 1.
-
Click Next to go to its definition.
Note: Observe that Model and Input Variables are already defined and derived from the earlier setup. Notice that all design variables in this study are controlled.
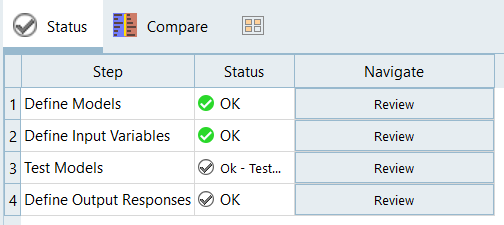
Figure 18.
-
Right-click in the Explorer browser area and from the context menu,
click Add to display the Add Approach
dialog.
-
Define test models.
-
Click Review to navigate to the Test
Model.
Figure 19. -
Click Run Definition to test the model
execution.
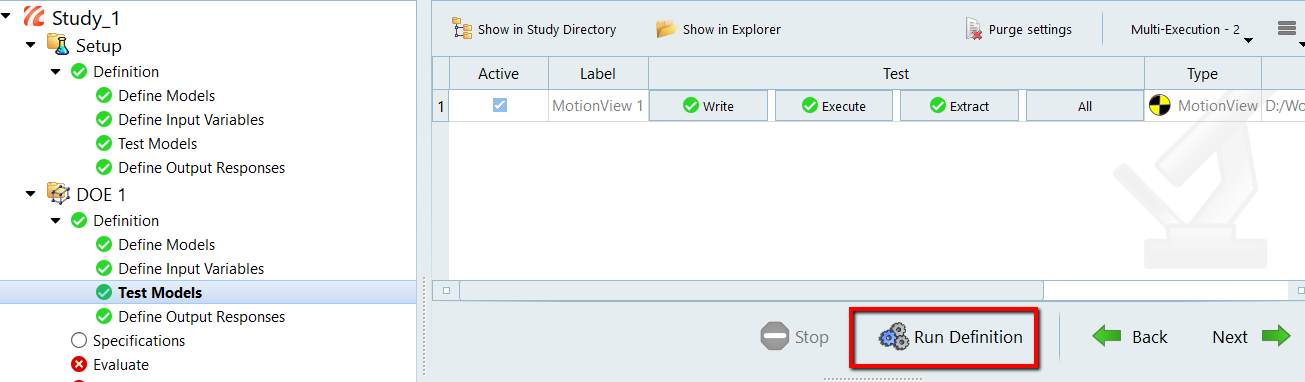
Figure 20.
-
Click Review to navigate to the Test
Model.
-
Select responses for the DOE study:
- There is only one response in the present study - make sure to select the response.
- Click Next to go to Specifications.
-
Specifications for the DOE study:
The design space for the DOE study is created in this step. The present study has four design variables with two levels each. A full factorial will give 24 = 16 experiments, as the number of experiments are less. We will do a full factorial run.
-
Click Show more... and select Full
Factorial mode,
 .
.
Figure 21.Note: Selecting any mode from the list shows all possible options in the Parameters panel area on the left side of GUI. -
Click the Levels tab to see the design variables
and number of levels.
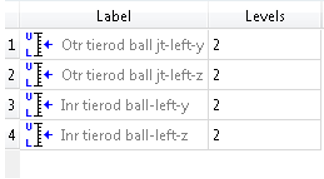
Figure 22. -
Click the Interaction tab to observe that it is
not applicable since all interactions are selected by default for a full
factorial run.
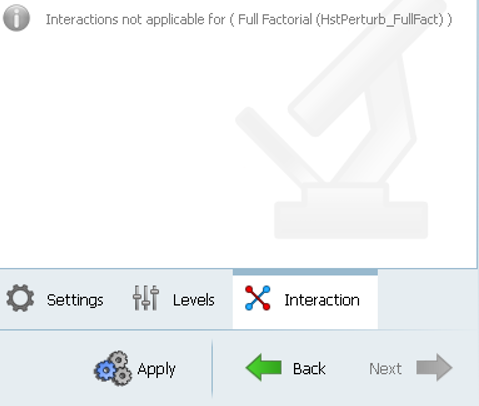
Figure 23.Note: Options which are not applicable will be grayed out or a message will be shown.
-
Click Show more... and select Full
Factorial mode,
- Click Apply to generate the design space.
- Click Next to go to Evaluate.
-
DOE run:
The Tasks tab of Evaluate shows a table of 16 rows and four columns. Column 1 shows the experiment number while other columns corresponding to each experiment get updated with the experiment status of failure or success in the three stages of model execution: Write, Execute and Extract.
Design variable values used under each experiment can be seen under the Evaluation Data tab.
The last column corresponds to the response value from each run. The values gets populated once the run is completed.
-
Click Evaluate Tasks to start the DOE
study.
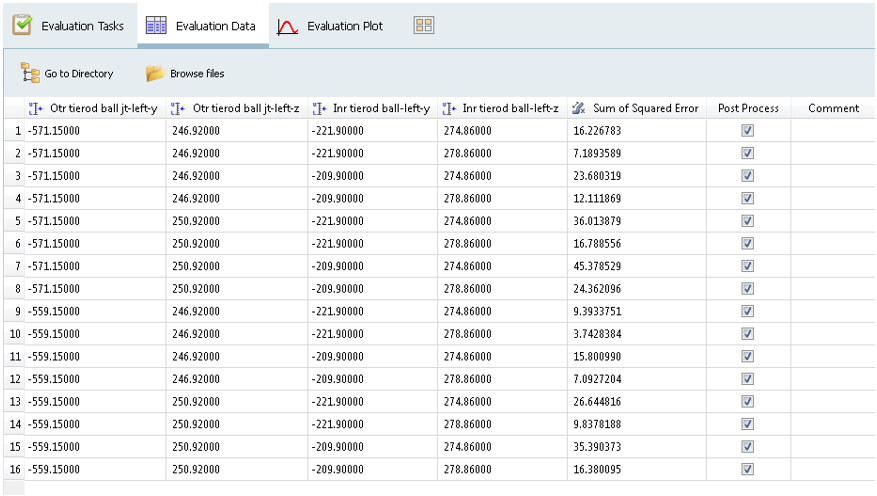
Figure 24.Once all the runs are finished, the tasks table gets filled up with the status for each run (Success/Fail).
- In the present DOE study, all runs are successfully completed. Click Next to go to Post Processing.
-
Click Evaluate Tasks to start the DOE
study.
-
Viewing Main Effect and Interaction plots:
The post-processing section has variety of utilities to helps user to effectively post process results. Summary tab of Post processing page will provide a summary of design along with responses.
The New Generation HyperStudy allows you to sort data by right-clicking on the column heading and selecting the options from context menu.
The options to post-process are available in other tabs. The main effects can be plotted by selecting the Linear Effects tab.
-
Main Effects
- Click the Linear Effects tab to open the main effects plot window. From the Channel page, select Variables and Responses for which main effects need to be plotted. Press the left mouse button and move over the variable or responses list for multiple selection.
-
Select all controlled variables and responses to plot the main effect
plot. This plot shows the effect of each parameter on the
response.
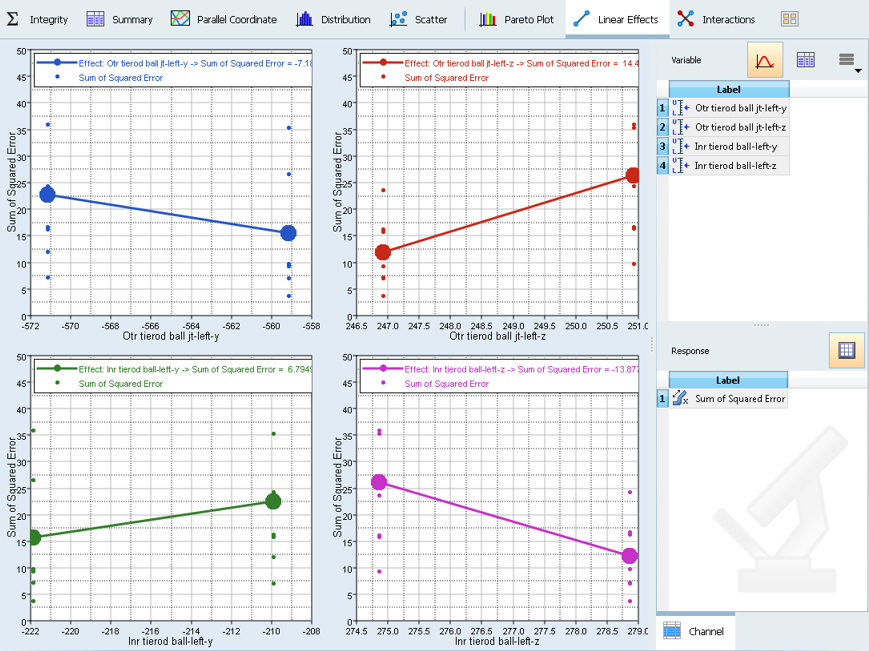
Figure 25. DOE – Main effects plotNote: Click on window icon, , (highlighted above) to toggle it to
multiple windows,
, (highlighted above) to toggle it to
multiple windows,  . Each curve is displayed in a different
plot window.
. Each curve is displayed in a different
plot window.
-
Interactions
An interaction is the failure of one variable to produce the same effect on the output response at different levels of another input variable. In other words, the strength or the sign (direction) of an effect is different depending on the value (level) of some other variable(s). An interaction can be either positive or negative.
Interactions can be plotted from the Interactions tab following the above procedure.
- Select the design variables Otr_tierod_ball_jt-left-z and Inr_tierod_ball_jt-left-z and response Sum of Squared Error.
-
Click the Interaction tab to observe that it is
not applicable since all interactions are selected by default for a full
factorial run.
This displays the interaction plot for these two variables only.
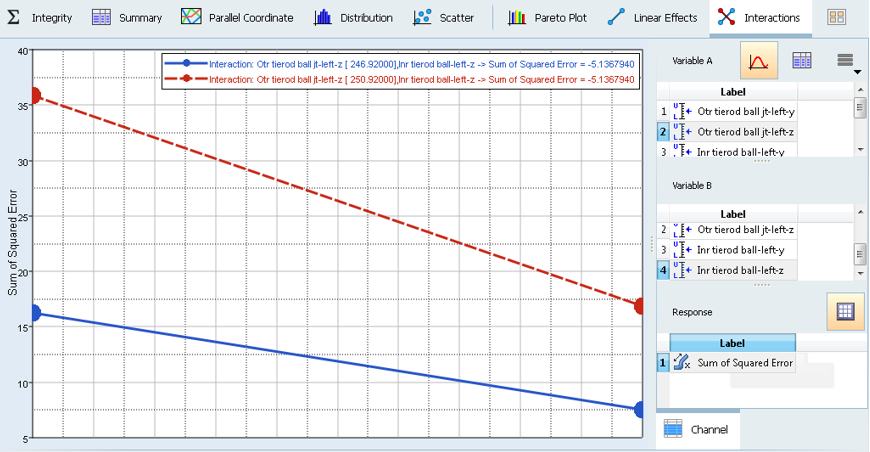
Figure 26. Controlled design variable plot for “Otr_tierod_ball_jt-left-z” & “Inr_tierod_ball_jt-left-z” interaction
Step 3: Approximation
System response is approximated by using various curve fitting methods. An approximation for the response with the design variables variation is calculated using the data from above DOE study. The accuracy of the approximation can be checked and improved.
-
Adding an approximation.
-
Right-click in the Explorer browser area and from the context menu,
click Add to display the Add Approach
dialog.
Figure 27. - Under Select Type, select Fit.
-
Accept the default label and variable names and click
OK.
A new tree with the name Fit 1 is created in the Browser.
-
Click Next to go to its definition.
Note: Model and Input Variables are already defined and derived from the earlier setup.
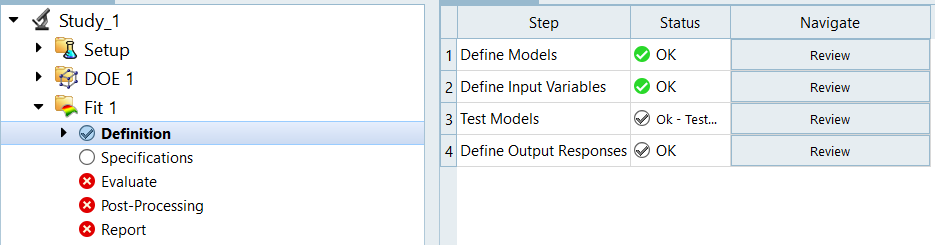
Figure 28. -
Define Test models. Click Review to navigate to
the Test Model. Click Run Definition to test
model execution.
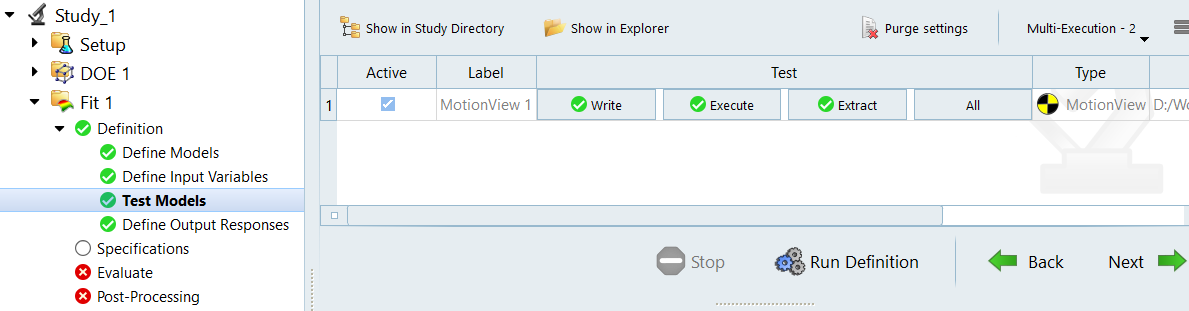
Figure 29. - Click Next to review Output Responses.
- Click Next to define specifications.
-
Right-click in the Explorer browser area and from the context menu,
click Add to display the Add Approach
dialog.
-
Define specifications.
-
Note: A matrix has already been added by default. Verify that the following options specify the DOE results, as the input matrix has been selected by default.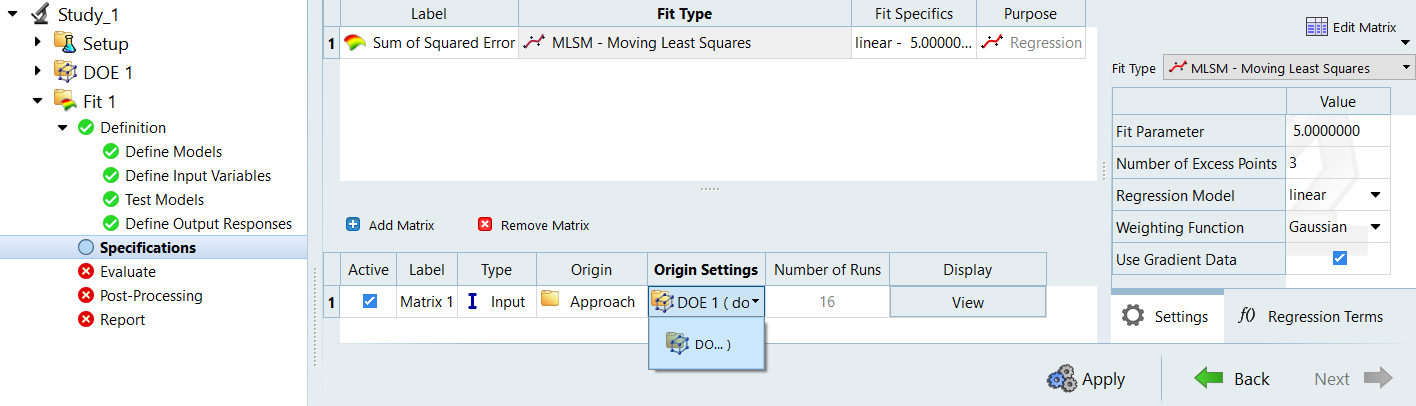
Figure 30. - Under Type, use the drop-down menu to select Input.
-
For Matrix Source, select Doe 1 from the
drop-down menu.
In the present study, we are not using any validation matrix. So, no matrix will be added for validation matrix.
- Click View under the Display column to review the run matrix. Close to return.
- Change the Fit type to Moving Least Squares and accept the defaults.
- Click Apply to apply the approximation method.
- Click Next to go to Evaluate.
- Observe an empty Tasks table which corresponds to the DOE experiments.
-
Click Evaluate Tasks to evaluate the
approximation for the DOE experiments.
Upon completion, the table is populated with the status value (Success or Fail).
- Click the other tabs available to observe the fit.
- Click the Evaluation Data tab to observe the experiment table with responses from the MotionSolve run and responses predicted using approximation. The same can be viewed in graph format by selecting the Evaluation plot tab.
-
Select Sum of Squared of Squared Error and
Squared of Squared Error_MLSM to plot against
the experiment numbers.
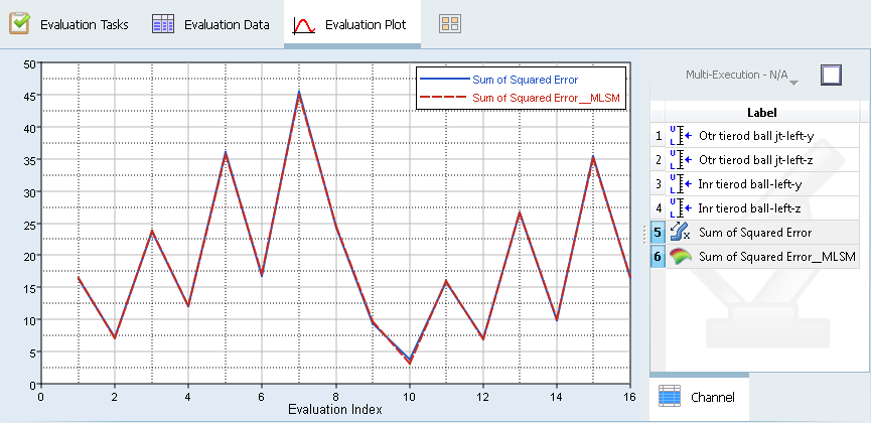
Figure 31.This fit shows a good approximation to the response.
-
Click Next to go to Post Processing.
Post-processing provides you with statistical parameters and graphical tools useful in validating the correctness of approximation.
The Residuals tab shows the difference between the response value from the solver and the response value from the regression equation.
The residual values can be used to determine which runs are generating more errors in the regression model.
The Trade-off tab shows the plots of the main effects vs. response from the approximation.
Figure 32. Trade-off: 3-D plots -
Select Otr_tierod_ball_jt-left-y as the X axis
and Otr_tierod_ball_jt-left-z as the Y axis to
plot against response from the approximation.
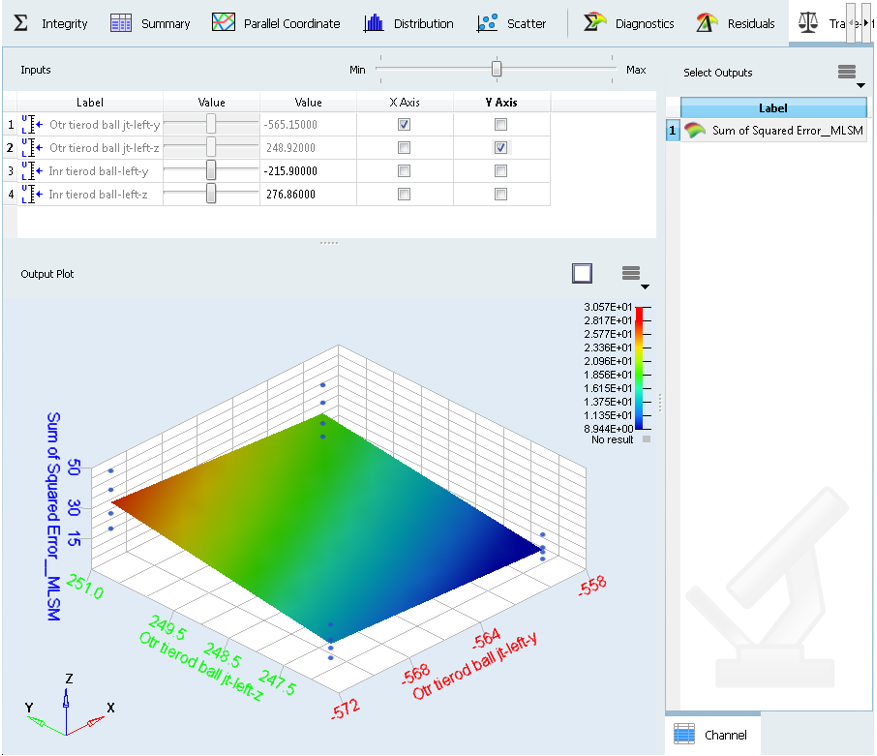
Figure 33. -
From the toolbar, click the Save icon,
 , to save the study.
Note: All study files will be saved in the study directory with the folder names that are the same as the tree varnames. For example, nom_1, doe_1, and fit_1.
, to save the study.
Note: All study files will be saved in the study directory with the folder names that are the same as the tree varnames. For example, nom_1, doe_1, and fit_1.
-