Herschel Bulkley Model |

|

|

|

|
|
Herschel Bulkley Model |

|

|

|

|
Regularized Herschel-Bulkley model is a four-parameter model and it is given by the following equation.

This model describes the viscosity using a power-law relationship and a yield criterion. The exponent n determines the nature of the power law relationship and the yield criterion is implemented using the regularized model with yield stress t0 and regularization parameter m. Higher the value of m, closer the approximation to the actual yield stress behavior of Herschel-Bulkley model. For practical purposes, value of m=10000 should be suffice. This regularization parameter controls the exponential growth of stress. The original Herschel-Bulkley model, which is given by the following equation, suffers from the disadvantage of stress growing very large when the shear rate tends to zero. This will lead to numerical instability and also increase the difficulty of obtaining a converged solution. Hence, this model is regularized using the parameter m.
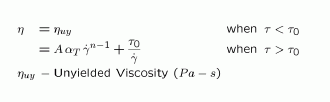
In addition to the above data, few additional parameters arise due the temperature dependence of material data; these variables are discussed in Section titled Temperature Dependence.
Syntax
Syntax of the data packet Polymer is as follows:
Polymer |
Polymer_name |
{ |
|
ConstitutiveModel = |
"HerschelBulkley" |
|
Density = |
ρ |
|
SpecificHeat = |
Cp(T) |
|
Conductivity = |
K(T) |
|
CoeffOfThermalExpansion = |
βΤ |
|
VolumetricHeatSource = |
Qvol |
|
Consistency = |
A |
|
Exponent = |
n |
|
YieldStress = |
τ0 |
|
StressExponentGrowth = |
m |
|
TemperatureDependence = |
"None"} |
Parameter |
Description |
Units |
Data Type |
Condition |
Typical Value |
ConstitutiveModel |
Describes the model used |
None |
String |
Required |
"HerschelBulkely" |
Density |
Density of the polymer |
kg/m^3 |
Constant |
Required |
995.0 |
SpecificHeat |
Specific heat at constant pressure |
J/kg/K |
Constant / F(T) |
Required |
2000.0 |
Conductivity |
Thermal conductivity |
W/m/K |
Constant / F(T) |
Required |
0.167 |
CoeffOfThermalExpansion |
Indicates the change in volume with change in temperature |
1/K |
Constant |
Required |
1.0e-05 |
VolumetricHeatSource |
Heat generated/ removed in the volume by methods like electrical heating |
W/m^3 |
Constant |
Required |
0.0 |
Consistency |
One of the parameters of the Herschel—Bulkley model. When n=1 it is same as viscosity. |
Pa s^n |
Constant |
Required |
1.0e+04 |
Exponent |
Power law index, defines the dependency of viscosity on shear rate. |
None |
Constant |
Required |
0.66 |
ZeroShearRateLimit |
See Power law model |
1/s |
Constant |
Required |
0.01 |
YieldStress |
One of the parameters of the Herschel—Bulkley model. |
Pa |
Constant |
Required |
1.0E+05 |
StressExponentGrowth |
One of the parameters of the Herschel—Bulkley model. It is also known as the regularization parameter. It controls the exponential growth of stress |
s |
Constant |
Required |
|
TemperatureDependence |
None |
String |
Required |
"Exp(-Beta(DeltaT))" |
|
ReferenceTemperature |
Temperature at which data is calculated for the initialization step. |
K |
Constant |
Required only if TD is not "None" |
533 |
FreezeTemperature |
This is the no flow temperature. Below this temperature, material ceases to flow. |
K |
Constant |
Required only if TD is not "None" |
350 |
ActivationEnergy |
A parameter required by Arrhenius model. |
J/mol |
Constant |
Required only if TD is Exp(Q/RT) |
16628 |
UniversalGasConstant |
A parameter from state equation PV = nRT, R is universal Gas constant. |
J/mol/K |
Constant |
Required only if TD is Exp(Q/RT) |
8.314 |
TemperatureSensitivity |
A derived parameter which has the same physical meaning as Q/R. |
K |
Constant |
Required only if TD is Exp(Tb/T) |
2000 K |
WLFConstant1 |
Constant C1 of WLF model |
None |
Constant |
Required only if TD is WLF |
17.44 |
WLFConstant2 |
Constant C2 of WLF model. This is like DeltaT, hence the value is same in K and Celsius. |
K |
Constant |
Required only if TD is WLF |
51.6 |
GlassTransitionTemperature |
Temperature below with polymer molecules ceases to move (frozen). There are few definitions of this term. |
K |
Constant |
Required only if TD is WLF |
320 |
Beta |
Parameter in the relationship Exp(-Beta(DeltaT)) |
None |
Constant |
Required only if TD is Exp(-Beta(DeltaT)) |
0.005 |
F(T) - Function of Temperature. Can be specified as a TABLE1 or TCL function.
TD - TemperatureDependence