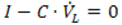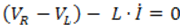Compose-4020：微分代数方程式の解法

連立方程式で代数微分方程式と常微分方程式の両方が使用されている場合、その連立方程式は微分代数方程式です。その解法は、常微分方程式とは異なります。その相違点は、ユーザー関数をどのように定義するか、および常微分方程式のように状態変数の導関数に初期条件を必要とするかどうかにあります。

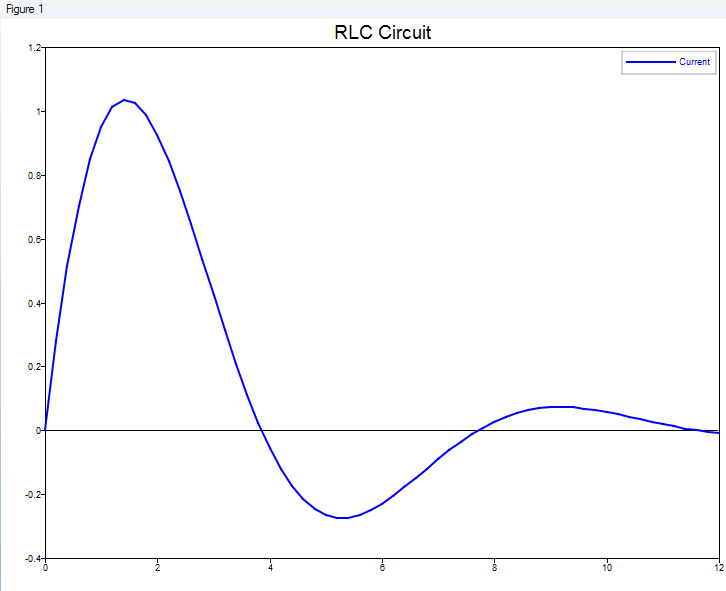
このチュートリアルでは、一定の電圧を印加する直列RLC回路を微分代数方程式として定式化することで、この回路を解きます。

変数は次のとおりです。
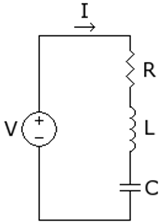
  • VR：抵抗とインダクタ間のノード電圧
  • VL：インダクタとコンデンサ間のノード電圧
  • V：電源電圧
  • I：回路電流
  • R：抵抗値
  • C：静電容量値
  • L：インダクタンス値

この回路を記述する連立方程式は次のようになります。

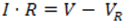
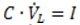
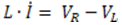
系の状態変数は、I、VR、およびVLです。これらの変数の時系列値を求めます。1番目の式は全面的に代数式であり、導関数を持ちません。これは、この系がODE系と明確に異なる点です。

方程式の書き直し

常微分方程式と異なり、微分代数系は次のように残差に関して書き直す必要があります。

方程式の実行

  1. Composeを開始します。
  2. ファイルメニューで、開くを選択して、<installation_dir>/tutorials/フォルダでファイルode15iDemo.omlを探します。

    この系の関数は次のようになります。このコードでは、ベクトル[i, VR, VL]をyで表記しています。

    回路の変数を定義します。

    この系を解くには、次の手順を実行します。

    1. ハンドルを使用して、DAEによるシステム関数に回路の変数を渡します。
    2. どの時間について系を解くかを定義します。
    3. y の[i, VR, VL]について初期値を定義します。
    4. yp の[i, VR, VL]の導関数の初期値を定義します。
    5. しきい値を設定します。わかりやすいように、次では明示的にデフォルト値を指定しています。
    6. 入力を指定してode15iを呼び出します。
    コードは次のようになります。

    1番目の出力引数として時間ベクトルが再生成されます。このチュートリアルでは入力と同じです。2番目の出力引数であるvには、ベクトルtに記述された時間ごとに、i、VR、VLの値が列単位で記述されます。

    次のコードでは、この結果を抽出してプロットします。