OS-E: 0930 Optimization Using Compose Function for DRESP3 Response
This example deals with a size optimization of a radar stiffened panel, where the response used as objective is an external response (DRESP3) using a function defined in Compose.

Figure 1. FE Model (including symmetries from post), and View of the Function Defined in Compose
Model Files
Refer to Access the Model Files to download the required model file(s).
The model files used in this example include:
- Optim_Size_Radar_Dresp3_MinCost.fem
- dresp3_cost_estimation.oml
Model Description
| FE Model | Shell Elements & Rigids Only ¼ of the panel is modeled, then constrained with symmetry conditions |
|
| Optimization variables | 18 Size variables | 1 discrete variable on Young modulus 17 continuous variables on thickness (1 for each component) |
| Optimization formulation |
|
Cost response is evaluated via a
DRESP3, using:
|
The objective is to find the optimal thickness for each part composing an aluminum radar stiffened panel in order to reduce its cost as much as possible, while preserving consistent performances.
The radar is composed of a curved panel with constant thickness, and 16 rectangular aluminum parts that are used as stiffeners. Each part can have its own thickness, and all parts are welded together.
All parts must share the same material. To evaluate the cost (not available by default in OptiStruct), a function is used to calculate it.
In this particular case, the cost of each part is a function of the material to be used, and for a given material, the cost/thickness curve has some brutal change of slope. Because of that, use either conditions or interpolation methods, which are not possible using DRESP2 (internal response based on function): use DRESP3 (external response based on function).
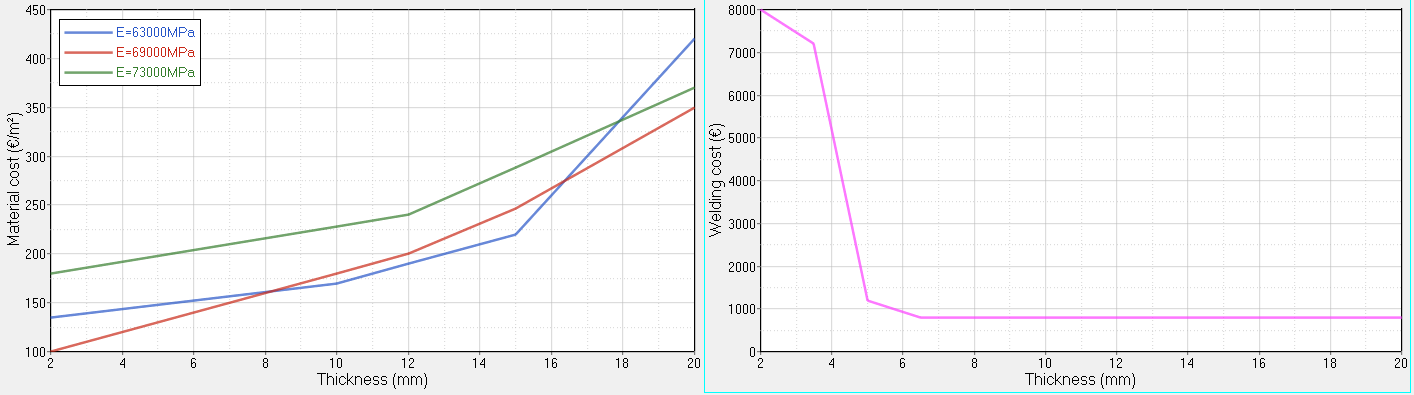
Figure 2. Evolution of Material Cost and Welding Process Cost for each Stiffening Part Depending on Thickness
In this example, Compose is used as the external tool to calculate the cost response.
The function, named “cost”, used the 17 thicknesses and the Young modulus as argument, and returns a single value: the global cost of the assembly, including the material cost and the welding cost.
Results
Due to the risk of local optimum, the use of multi-start (using GLOBAL card) is used here, with 10 different starting points.
Optimization runs in a little less than 8 minutes, and though it returns several solutions concerning thicknesses, all solution found uses the 69 000 MPa aluminum.
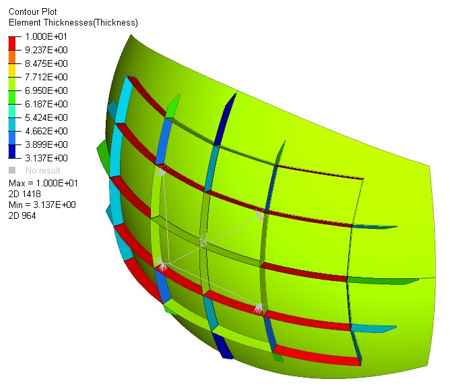
Figure 3. Thickness Distribution on Optimal Design
- Max von Mises
- =193 MPa < 200 MPa
- Max Displacement
- =49mm < 50 mm