Heat Transfer Between Radiating Concentric Spheres
In this application, AcuSolve is used to simulate the heat transfer due to conduction and radiation between concentric spheres. The inside surface of the inner and the outside surface of the outer sphere are both held at constant temperature, while the gap between them radiates the heat from one sphere to the other.
AcuSolve results are compared with analytical results for temperature and heat flux as described in Incropera (2006) and Salazar, et al. (2016). The close agreement of AcuSolve results with analytical results validates the ability of AcuSolve to model cases with radiation heat transfer and conjugate heat transfer with enclosure radiation modeling and the discrete ordinate (DO) radiation model.
Problem Description

Figure 1. Critical Dimensions and Parameters used for Simulating Conduction and Radiation Between two Concentric Spheres

Figure 2. Mesh used for Simulating Radiation Between two Concentric Spheres
The simulation was performed as a three dimensional problem by constructing a volume mesh that contains a layer of boundary elements normal to the radial direction.
AcuSolve Results
| T(r1) (K) | T(r2) (K) | Q(r1) (W) | Q(r2) (W) | |
|---|---|---|---|---|
| Analytical | 578.2 | 1035.0 | -27822.5 | 12365.6 |
| AcuSolve (Enclosure) | 578.4 | 1035.1 | -27827 | 12364.2 |
| AcuSolve (DO) | 561.8 | 1023.6 | -26175 | 12897.0 |
| Percent Difference (Enclosure) | 0.034% | 0.010% | -0.015% | -0.011% |
| Percent Difference (DO) | 2.8% | -1.11% | 5.92% | 4.3% |
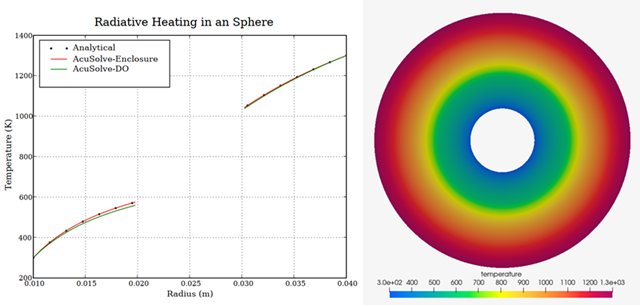
Figure 3. Two-Dimensional Plot and Contours of Temperature Between the Concentric Spheres
Summary
The AcuSolve solution compares well with analytical results for heat transfer due to conduction and radiation between two concentric spheres. In this application, an arbitrary material is subjected to a heat flux that is calculated based on the view factors or the DO model within the simulation. As a result of the conjugate heat transfer and the radiative heat flux a temperature distribution between the two spheres develops. The AcuSolve solution for the temperature and heat flux at the radiation surfaces matches well compared to the analytical solution with only a minor difference for the enclosure radiation model. The enclosure radiation model was found to have a higher accuracy for this application compared to the DO model, as expected due to the relatively low optical thickness in this simulation.
Heat Transfer Between Radiating Concentric Spheres
HyperWorks CFD database file: <your working directory>\sphere_radiation\sphere_radiation.hm.
Global
- Problem Description
- Analysis type - Steady State
- Turbulence equation - Advective Diffusive
- Radiation equation - Enclosure
- Auto Solution Strategy
- Convergence tolerance - 1.0e-5
- Relaxation Factor - 0.4
- Flow - off
- Enclosure radiation - on
- Material Model
- Inner
- Conductivity
- Type - Constant
- Conductivity - 2.0
- Outer
- Conductivity
- Type - Constant
- Conductivity - 0.35
- Radiating
- Conductivity
- Type - Constant
- Conductivity - 1.0e-6
- Emissivity Model
- Inner
- Emissivity - 0.5
- Outer
- Emissivity - 0.8
Model
- Volumes
- Inner
- Element Set
- Medium- Solid
- Material model - Inner
- Outer
- Element Set
- Medium - Solid
- Material model - Outer
- Element Set
- Radiating
- Element Set
- Medium - Fluid
- Material model - Radiating
- Element Set
- Element Set
- Inner
- Surfaces
- Inner_Inner_r1
- Simple Boundary Condition - (disabled to allow for heat flux)
- Inner_Inner_ri
- Simple Boundary Condition
- Type - Wall
- Temperature BC type - Value
- Temperature - 300.0 K
- Simple Boundary Condition
- Inner_Radiating_r1
- Simple Boundary Condition (disabled to allow for heat flux)
- Radiation Surface
- Type - Wall
- Emissivity model - Inner
- Outer_Outer_r2
- Simple Boundary Condition (disabled to allow for heat flux)
- Inner_Outer_ro
- Simple Boundary Condition
- Type - Wall
- Temperature BC type - Value
- Temperature - 1300.0 K
- Simple Boundary Condition
- Outer_Radiating_r2
- Simple Boundary Condition (disabled to allow for heat flux)
- Radiation Surface
- Type - Wall
- Emissivity model - Outer
- Inner_Inner_r1
References
F. P. Incropera and D. P. DeWitt. "Fundamentals of Heat Transfer – Sixth Edition". John Wiley & Sons. New York. 2006.
Salazar, G., Droba, J., Oliver, B., & Amar, A. J. (2016). Development and Verification of Enclosure Radiation Capabilities in the CHarring Ablator Response (CHAR) code. 46th AIAA Thermophysics Conference.