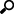|
Slope
The slope of the least-squares line.
The formula:
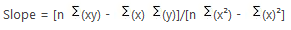
Sample 1:
Give the set of X and Y values where X and Y can represent any correlated values below:
|
X |
Y |
|
1 |
2 |
|
2 |
4 |
|
3 |
6 |
|
4 |
8 |
|
5 |
10 |
|
6 |
12 |
|
7 |
14 |
|
8 |
16 |
|
9 |
18 |
|
10 |
20 |
Sample table
Computing the Slope
-
Solve the parts of the formula:
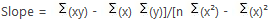
n =count of items, equal to 10
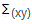= multiply
all x and y items and get the sum = 770
1x2 + 2x4 + 3x6 + 4x8 + 5x10 + 6x12 + 7x14 + 8x16 + 9x18 + 10x20 = 770
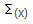= sum
of x items = 55
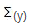= sum
of y items = 110
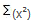= get
the square of all x items and sum up the values. To square a number also
means to multiply the number by itself.
1x1 + 2x2 + 3x3 + 4x4 + 5x5 + 6x6 + 7x7 + 8x8 + 9x9 + 10x10 = 385
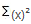= get the sum of
all items in x and get the square = 55 * 55 or 3025
-
Substitute the known values in the formula and computed for the Slope:
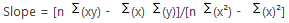
Slope = [10(770) – 55(110)]/[10(385) – 3025]
Slope = [7700 – 6050]/3850-3025]
Slope = 1650/825
Slope = 2