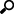HarmonicMean
The harmonic mean gives equal weight to each data point, meaning that extreme outlier values will not impact the Harmonic Mean as much as it would an Arithmetic Mean.
Typically, it is appropriate for situations when the average of rates is desired. The Harmonic mean H of the positive real numbers x1, x2, ..., xn > 0 is defined to be
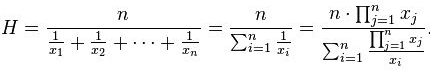
Sample 1:
As a simple example, the Harmonic mean of 1, 2, and 4 is:
Sample 2:
Another example based on the number of hours worked per week:
The table shows the average working hours per week per employee (a rate). Each employee was only required to work 2000 hours but their working hours differs per week:
|
Employee |
Total Hours Worked |
Average Working Hours Per Week |
Work Weeks |
|
Joy |
2000 |
50 |
40 |
|
Thomas |
2000 |
45 |
44.4444 |
|
Erick |
2000 |
35 |
57.142857 |
|
John |
2000 |
40 |
50 |
Employee working hours per week
The total number of working hours by all four employees is 8000 hours. The total number of work weeks is 191.59 weeks. The calculation to compute for the Harmonic mean is:
4/(1/50 + 1/45 + 1/35 + 1/40) = 41.7564 hours
A simple check of dividing 8000 hours by 41.76 will equal 191.59 which is the total number of weeks the employees worked.