Mathematical Background
This section on mathematical background covers the various notations and operators used to formulate and define the equations of fluid flow.
Vector or Dyadic Notation
The conservation laws for a continuum medium involve vector and tensor quantities as well as several operators such as gradient and divergence.
In order to have a comprehensive understanding of these equations it is essential to get a good grasp of the notations and operators used in this manual.
In this notation, the governing equation is independent of the choice of the coordinate system. For the purposes of this manual the scalar quantities would be denoted with italicized letters. For example, pressure field is denoted as . The vector quantities would be denoted with an arrow above the letters, for example velocity field denoted as . Tensor quantities are donated with bold face letters, for example stress tensor represented as .
Cartesian Tensor Notation
In this notation, an index subscript is written after the quantity which corresponds to a component of the quantity.
Single subscript is used to denote a component of vector, for example for the vector field and two subscripts are used to denote a component of tensor, for example for the stress tensor .
Kroneker Delta
The Kroneker Delta is a second-order isotropic tensor which is defined as: , .
Operators
The most frequently used math operator related to flow equations is the referred to as nabla, grad or del.
appears in several different ways when applied to scalar, vector and tensor quantities.
Gradient
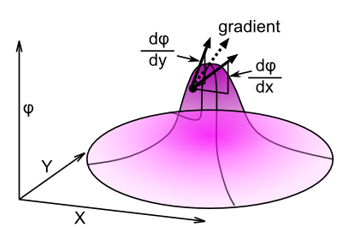
Figure 1. Gradient at a Point
The gradient of a vector quantity represents the gradient of each component of the vector field individually, each of which is a scalar.
Divergence

Figure 2. Divergence at a Point
Div
It maps a vector quantity to a scalar which can then be applied to a scalar, vector or higher order tensors.
Laplacian
Double Dot Product (Scalar Product of Two Tensors)
Total Derivative
The total derivative of a quantity can be seen as a sum of local time derivative and convective derivative.